题目内容
当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为80°,那么这个“特征三角形”各个内角的度数分别为 、 、 .
考点:三角形内角和定理
专题:新定义,分类讨论
分析:根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.
解答:解:由题意得:α=2β,α=80°,则β=40°,
180°-80°-40°=60°,
故答案为:80°,40°,60°.
180°-80°-40°=60°,
故答案为:80°,40°,60°.
点评:此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
下面与
是同类二次根式的是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.
已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.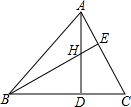 如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.
如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.