ΧβΡΩΡΎ»ί
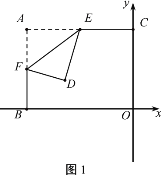
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒxoy÷–Θ§A(Θ≠4Θ§3)Θ§Ζ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΖ÷±πΫΜΨΊ–ΈABOCΒΡΝΫ±ΏACΘ§BC”ΎEΘ§FΘ®EΘ§F≤Μ”κA÷ΊΚœΘ©Θ§―ΊΉ≈EFΫΪΨΊ–ΈABOC’έΒΰ ΙAΘ§D÷ΊΚœΘ°
ΒΡΆΦœσΖ÷±πΫΜΨΊ–ΈABOCΒΡΝΫ±ΏACΘ§BC”ΎEΘ§FΘ®EΘ§F≤Μ”κA÷ΊΚœΘ©Θ§―ΊΉ≈EFΫΪΨΊ–ΈABOC’έΒΰ ΙAΘ§D÷ΊΚœΘ°
 ΓΓΓΓΓΓΓΓΓΓ
ΓΓΓΓΓΓΓΓΓΓ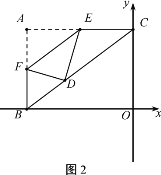
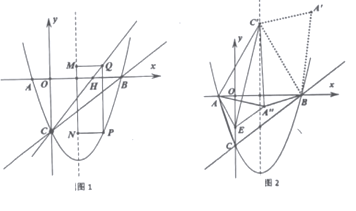
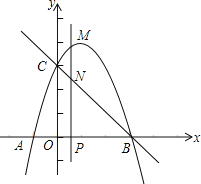
Θ®1Θ©ΔΌ»γΆΦ2Θ§Β±ΒψD«ΓΚΟ‘ΎΨΊ–ΈABOCΒΡΕ‘Ϋ«œΏBC…œ ±Θ§«σCEΒΡ≥ΛΘΜ
ΔΎ»τ’έΒΰΚσΒψD¬δ‘ΎΨΊ–ΈABOCΡΎΘ®≤ΜΑϋά®±ΏΫγΘ©Θ§«σœΏΕΈCE≥ΛΕ»ΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®2Θ©»τ’έΒΰΚσΘ§ΓςABD «Β»―ϋ»ΐΫ«–ΈΘ§«κ÷±Ϋ”–¥≥ω¥Υ ±ΒψDΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌECΘΫ2ΘΜ ΔΎ![]() ΘΜΘ®2Θ©ΒψDΒΡΉχ±ξΈΣ
ΘΜΘ®2Θ©ΒψDΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΗυΨίA(Θ≠4Θ§3)ΚΆΖ¥±»άΐΚ· ΐΆΦœσ…œΒψΒΡΧΊ’ςΩ…ΒΟEΓΔFΒΡΉχ±ξΘ§¥”ΕχΩ…±μ Ψ≥ωAEΓΔAF≤Δ«σΒΟ![]() Θ§¥”Εχ÷ΛΒΟΓςAEFΓΉΓςACBΘ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΡ’έΒΰΒΡ–‘÷ Ω…ΆΤ≥ω
Θ§¥”Εχ÷ΛΒΟΓςAEFΓΉΓςACBΘ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΡ’έΒΰΒΡ–‘÷ Ω…ΆΤ≥ω![]() Θ§Φ¥Ω…«σΒΟΫαΙϊΘΜ
Θ§Φ¥Ω…«σΒΟΫαΙϊΘΜ
ΔΎΒ±D‘ΎBO…œ ±Θ§”…’έΒΰΒΡ–‘÷ ΚΆΆ§Ϋ«ΒΡ”ύΫ«œύΒ»÷ΛΒΟΓςAEFΓΉΓςBADΘ§…ηAF=xΘ§άϊ”ΟΙ¥Ι…Ε®άμΩ…Ν–≥ωΖΫ≥ΧΘ§Ϋβ÷°ΒΟAFΒΡ≥ΛΘ§ΫχΕχ«σ≥ωAEΓΔCEΒΡ≥ΛΘ§Φ¥Ω…ΒΟ≥ωCEΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©”…ΓςABD «Β»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟ![]() Μρ
Μρ![]() Θ§Ζ÷«ιΩωΫχ––«σΫβΦ¥Ω…Θ°
Θ§Ζ÷«ιΩωΫχ––«σΫβΦ¥Ω…Θ°
Ϋβ:Θ®1Θ©ΔΌ”…Χβ“βΒΟ![]() Θ§
Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ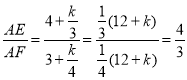 Θ§
Θ§
ΓΏ”…A(Θ≠4Θ§3)ΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏΓœA=ΓœAΘ§
ΓύΓςAEFΓΉΓςACBΘ§
ΓύΓœAEF=ΓœACBΘ§
ΓύEFΓΈCBΘ§
»γΆΦ2Θ§Ν§Ϋ”ADΫΜEF”ΎΒψH Θ§
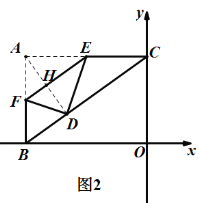
”…’έΒΰΒΡ–‘÷ ΒΟΘΚAH=DHΘ§
ΓΏD‘ΎBC…œΘ§
Γύ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
ΔΎ”…’έΒΰΒΟEF¥Ι÷±ΤΫΖ÷ADΘ§
Γύ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
»γΆΦΘ§Β±D¬δ‘ΎBO…œ ±Θ§ΓΏ![]() Θ§
Θ§
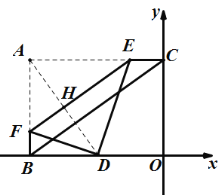
ΓύΓςAEFΓΉΓςBADΘ§
Γύ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
…ηAF=xΘ§‘ρFB=3Θ≠xΘ§FD=AF=xΘ§
‘ΎRtΓςBDF÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚ![]() Θ§
Θ§
Φ¥![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§Φ¥’έΒΰΚσΒψD¬δ‘ΎΨΊ–ΈABOCΡΎΘ®≤ΜΑϋά®±ΏΫγΘ©Θ§CEΒΡ»Γ÷ΒΖΕΈßΈΣ
Θ§Φ¥’έΒΰΚσΒψD¬δ‘ΎΨΊ–ΈABOCΡΎΘ®≤ΜΑϋά®±ΏΫγΘ©Θ§CEΒΡ»Γ÷ΒΖΕΈßΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏΓςABD «Β»―ϋ»ΐΫ«–ΈΘ§œ‘»Μ![]() Θ§
Θ§
Γύ![]() Μρ
Μρ![]() Θ§
Θ§
ΔΌΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
”…Θ®1Θ©ΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
»γΆΦΘ§ΙΐΒψDΉς![]() ÷αΖ÷±πΫΜABΓΔy÷α”ΎΒψMΓΔNΘ§
÷αΖ÷±πΫΜABΓΔy÷α”ΎΒψMΓΔNΘ§
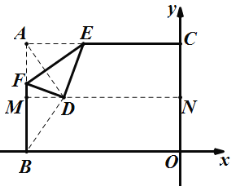
‘ρ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
ΓύΓςAEFΓΉΓςMBDΘ§
Γύ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύΒψDΒΡΉχ±ξΈΣ![]() ΘΜ
ΘΜ
ΔΎΒ±![]() ±Θ§»γΆΦΘ§ΙΐΒψDΉς
±Θ§»γΆΦΘ§ΙΐΒψDΉς![]() ÷αΖ÷±πΫΜABΓΔy÷α”ΎΒψMΓΔNΘ§
÷αΖ÷±πΫΜABΓΔy÷α”ΎΒψMΓΔNΘ§
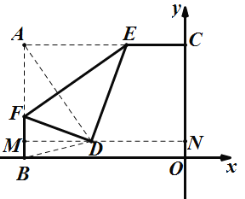
‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”…Θ®1Θ©ΒΟ![]() Θ§
Θ§
ΓύΓςAEFΓΉΓςMADΘ§
Γύ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
‘ΎRtΓςMAD÷–Θ§”…Ι¥Ι…Ε®άμΒΟΘΚ![]() Θ§
Θ§
Φ¥![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
ΓύΒψDΒΡΉχ±ξΈΣ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§»τ’έΒΰΚσΘ§ΓςABD «Β»―ϋ»ΐΫ«–ΈΘ§ΒψDΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]() Θ°
Θ°