��Ŀ����
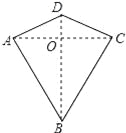
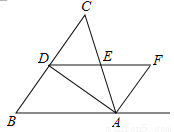
�����ڱ߷ֱ���ȵ��ı��ν��������Ρ�����ͼ���ı���ABCD��һ�����Σ�����AD=CD��AB=CB����̽�����ε�����ʱ���õ����½��ۣ��١�ABD�ա�CBD����AC��BD�����ı���ABCD�����=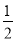 AC•BD��������ȷ�Ľ����У� ��
AC•BD��������ȷ�Ľ����У� ��
A. 0�� B. 1�� C. 2�� D. 3��
D ������������������ڡ�ABD���CBD�У� ���ɵá�ABD�ա�CBD��SSS�����ʢ���ȷ�� ����ȫ�������ε����ʣ��ɵá�ADB=��CDB���ڡ�AOD���COD�У� ���ɵá�AOD�ա�COD��SAS�����ɵá�AOD=��COD=90�㣬AO=OC�����ݴ�ֱ�Ķ���ɵ�AC��DB���ʢ���ȷ�� �ı���ABCD�����= =ACBD���ʢ���ȷ�� ��ѡD��
��ϰ��ϵ�д�
�����Ŀ


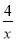 ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�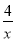 �ĸ��ʣ�
�ĸ��ʣ�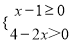 �Ľ⼯�������ϱ�ʾΪ��������
�Ľ⼯�������ϱ�ʾΪ��������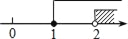 B.
B. 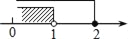
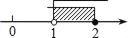 D.
D. 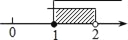
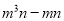 ����
����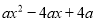 ��
��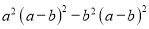 ����
����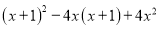 ��
��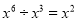 ����
����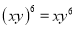 ����
����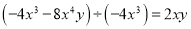 ����
����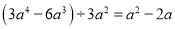 �����м��㲻��ȷ����( )
�����м��㲻��ȷ����( )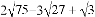 �Ľ����_____________.
�Ľ����_____________.