题目内容
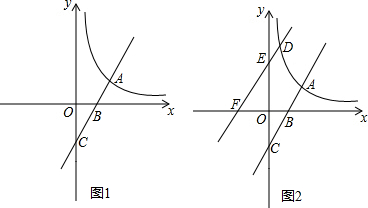
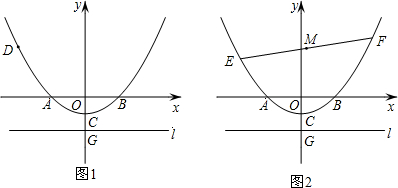
1.已知如图1,在以O为原点的平面直角坐标系中,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,-1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<-1.(1)求抛物线对应的二次函数的解析式;
(2)①若D(-4,m)为抛物线y=$\frac{1}{4}$x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值;
②若为抛物线y=$\frac{1}{4}$x2+bx+c上一动点,点D到①中的直线l的距离与OD的长是否恒相等,说明理由;
(3)如图2,若E,F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.
分析 (1)根据点C坐标,可得c=-1,然后根据AO=2CO,可得出点A坐标,将点A坐标代入求出b值,即可得出函数解析式;
(2)①设出点D坐标,分别求出OD和点D到直线l的距离,然后列出等式求出t的值;
②利用勾股定理得出OD2的值,进而得出答案;
(3)作EN⊥直线l于点N,FH⊥直线l于点H,设出点E、F坐标,表示出点M的纵坐标,根据(2)中得出的结果,代入结果求出M纵坐标的最小值.
解答 解(1)∵AO=2CO,C(0-1),
∴OA=2,A(-2,0),
将(0,-1),(-2,0)代入y=$\frac{1}{4}$x2+bx+c得:
$\left\{\begin{array}{l}{c=-1}\\{1-2b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=0}\\{c=-1}\end{array}\right.$
故抛物线解析式为:y=$\frac{1}{4}$x2-1;
(2)①由抛物线得:y=$\frac{1}{4}$×42-1=3,
故D(-4,3)
则OD=5,
又∵d=DO
∴t=3-5=-2,
②设D(a,$\frac{1}{4}$a2-1)
则OD2=a2+($\frac{1}{4}$a2-1)2
=a2+$\frac{1}{16}$a4-$\frac{1}{2}$a2+1
=($\frac{1}{4}$a2+1)2,
点D到直线l的距离:$\frac{1}{4}$a2-1+2=$\frac{1}{4}$a2+1,
故d=DO;
(3)作EN⊥直线l于点N,FH⊥直线l于点H,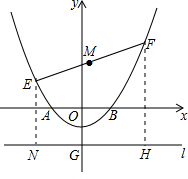
设E(x1,y1),F(x2,y2),
则EN=y1+2,FH=y2+2,
∵M为EF中点,
∴M纵坐标为:$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{(EN-2)+(FH-2)}{2}$=$\frac{EN+FH}{2}$-2,
由(2)得:EN=OE,FH=OF,
∴$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{EN+FH}{2}$-2=$\frac{OE+OF}{2}$-2,
要使M纵坐标最小,即$\frac{OE+OF}{2}$-2最小,
当EF过点O时,OE+OF最小,最小值为8,
∴M纵坐标最小值为$\frac{OE+OF}{2}$-2=$\frac{8}{2}$-2=2.
点评 本题考查了二次函数的综合知识,涉及到抛物线解析式的求法,点到直线的距离、两点间的距离等知识,涉及到的知识点比较多,利用数形结合表示出M点纵坐标是解题关键.

| A. | y=-(x+2)2-1 | B. | y=-(x-2)2-1 | C. | y=-(x-2)2+1 | D. | y=-(x+2)2+1 |
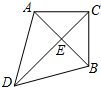 如图,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等边三角形,求CD的长度.
如图,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等边三角形,求CD的长度.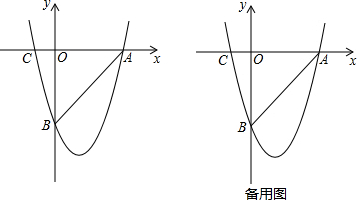
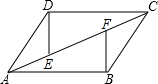 已知CD=AB,CD∥AB,AE=CF,求证:AD∥BC.
已知CD=AB,CD∥AB,AE=CF,求证:AD∥BC.