题目内容
18.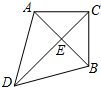 如图,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等边三角形,求CD的长度.
如图,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等边三角形,求CD的长度.
分析 由勾股定理求出AB,由等边三角形的性质得出AB=AD=BD=2,∠DAB=∠ABD=60°.证出AB⊥CD于E,且AE=BE=1.求出AE=CE=1,由勾股定理求出DE,即可得出结果.
解答 解:∵∠ACB=90°,AC=BC=$\sqrt{2}$,
∴由勾股定理,得 AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2.
∠CAB=∠CBA=45°.
∵△ABD是等边三角形,
∴AB=AD=BD=2,∠DAB=∠ABD=60°.
∵AC=BC,AD=BD,
∴AB⊥CD于E,且AE=BE=1.
在Rt△AEC中,∠AEC=90°,∠EAC=45°,
∴∠EAC=∠ACE=45°.
∴AE=CE=1.
在Rt△AED中,∠AED=90°,AD=2,AE=1,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{3}$.
∴CD=$\sqrt{3}$+1.
点评 本题考查了勾股定理、等腰直角三角形的性质、等边三角形的性质、线段垂直平分线的判定等知识;熟练掌握等边三角形和等腰直角三角形的性质,运用勾股定理求出DE是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列计算中,正确的是( )
| A. | (a2)3=a8 | B. | a8÷a4=a2 | C. | a3+a2=a5 | D. | a2•a3=a5 |
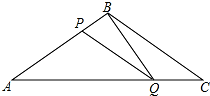 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
 如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.
如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF. 如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.