题目内容
2.如图,抛物线y=-x2+bx+c与x轴正半轴交于A点,与y轴正半轴交于B,直线AB的解析式为y=-x+3.(1)求抛物线解析式;
(2)P为线段OA上一点(不与O、A重合),过P作PQ⊥x轴交抛物线于Q,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;
(3)在(2)的条件下,连接QN并延长交y轴于E,连接AE,求t为何值时,MN∥AE.
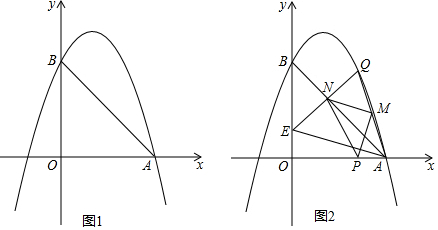
分析 (1)求出A、B两点坐标,利用待定系数法即可解决问题.
(2)如图1中,过点M作MG⊥x轴于G,NH⊥GM,于H.首先证明N、P、A三点在以M为圆心MA为半径的⊙M上,再根据△NMH≌△MPG,得到NH=MG,HM=PG,即可解决问题.
(3)如图2中,MN∥AE,QM=MA,得EN=QN,利用中点坐标公式,列出方程即可解决问题.
解答 解:(1)∵直线AB的解析式为y=-x+3,
∴A(3,0),B(0,3),
∵抛物线y=-x2+bx+c经过A点,B点,
∴$\left\{\begin{array}{l}{c=3}\\{-9+3b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3.
(2)如图1中,过点M作MG⊥x轴于G,NH⊥GM,于H.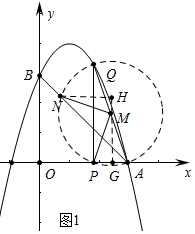
∵OA=OB,∠AOB=90°,
∴∠PAN=45°,
∵∠NMP=90°,
∴∠PAN=$\frac{1}{2}$∠NMP,
∴N、P、A三点在以M为圆心MA为半径的⊙M上,
∴MN=MP,
∵∠NHM=∠PGM=∠NMP=90°,
∴∠NMH+∠PMG=90°,∠PMG+∠MPG=90°,
∴∠NMH=∠MPG,
∴△NMH≌△MPG,
∴NH=MG,HM=PG,
∵P(t,0),
∴Q(t,-t2+2t+3),M($\frac{3+t}{2}$,$\frac{-{t}^{2}+2t+3}{2}$),
∴PG=MH=$\frac{3+t}{2}$-t=$\frac{3-t}{2}$,HG=$\frac{3-t}{2}$+$\frac{-{t}^{2}+2t+3}{2}$=$\frac{-{t}^{2}+t+6}{2}$,
∴Ny=$\frac{-{t}^{2}+t+6}{2}$,
∵点N在直线AB上,
∴Ny=-Nx+3,
∴Nx=3-$\frac{-{t}^{2}+t+6}{2}$=$\frac{{t}^{2}-t}{2}$(0<t<3).
(3)如图2中,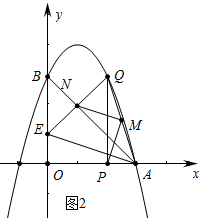
∵MN∥AE,QM=MA,
∴EN=QN,
∴$\frac{{t}^{2}-t}{2}$=$\frac{t}{2}$,
∴t2-2t=0,
解得t=2或0(舍弃),
∴t=2时,MN∥AE.
点评 本题考查二次函数综合题、圆、全等三角形的判定和性质、平行线等分线段定理、中点坐标公式等知识,解题关键是熟练掌握待定系数法确定函数解析式,学会利用圆,解决线段相等问题,属于中考压轴题.

| A. | 1200(1+x2)=1500 | B. | 1200(1+x)2=1500 | C. | 1200(1+2x)=1500 | D. | 1200(1+x)x2=1500 |
| A. | x-y=3 | B. | xy-3=1 | C. | x+$\frac{2}{y}$=5 | D. | x2-3y=0 |
| A. | 1.25×109 | B. | 0.125×1010 | C. | 12.5×108 | D. | 1.25×1010 |
 如图,梯形ABCD的中位线MN与对角线BD,AC分别交于E,F,EF:MN=1:2,AD=4,求BC的长.
如图,梯形ABCD的中位线MN与对角线BD,AC分别交于E,F,EF:MN=1:2,AD=4,求BC的长.