题目内容
14．已知△ABC中，AB=BC=4，AC=3，作与△ABC只有一条公共边，且与△ABC全等的三角形共有7个．分析 依照题意画出图形，利用数形结合数出与△ABC全等的三角形的个数，即可得出结论．
解答 解：依照题意画出图形，如图所示．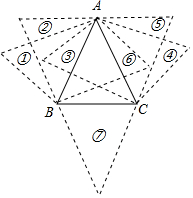
结合图形即可得知：与△ABC全等的三角形共有7个．
故答案为：7．
点评 本题考查了全等三角形的判定，根据题意画出图形利用数形结合找出与已知图形全等的三角形的个数是解题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
5．下列各对数互为相反数的是（ ）
| A． | 4和-（-4） | B． | -3和$\frac{1}{3}$ | C． | -2和-$\frac{1}{2}$ | D． | 0和0 |
9．用加减消元法解方程组$\left\{\begin{array}{l}{3x-2y=2}\\{x+y=5}\end{array}\right.$，下列变形正确的是（ ）
| A． | $\left\{\begin{array}{l}{3x-y=2}\\{x+2y=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{3x-2y=2}\\{x+2y=5}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{3x-2y=2}\\{3x+3y=15}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{3x-2y=2}\\{2x+2y=5}\end{array}\right.$ |
19．下列方程：
（1）-x2+2=0；（2）2x2-3x=0；（3）-3x2=0；（4）x2+$\frac{1}{x}$=0；（5）$\frac{{{x^2}+3}}{2}$+5x=0；（6）2x2-1=2（x-2）（x+1）+5x中
一元二次方程有（ ）
（1）-x2+2=0；（2）2x2-3x=0；（3）-3x2=0；（4）x2+$\frac{1}{x}$=0；（5）$\frac{{{x^2}+3}}{2}$+5x=0；（6）2x2-1=2（x-2）（x+1）+5x中
一元二次方程有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
3．下列命题中，正确的是（ ）
| A． | 圆心角相等，所对的弦相等 | B． | 三点确定一个圆 | ||
| C． | 长度相等的弧是等弧 | D． | 弦的垂直平分线必经过圆心 |
4．
按照图中的方法作图，作出的是（ ）
按照图中的方法作图，作出的是（ ）| A． | 一个角等于已知角 | B． | 一条线段等于已知线段 | ||
| C． | 线段的垂直平分线 | D． | 角的平分线 |