题目内容
15.$\sqrt{(-4)^{2}}$=4;(1-$\sqrt{5}$)($\sqrt{5}$+1)+($\sqrt{5}$-1)2=2-2$\sqrt{5}$.分析 利用二次根式的性质计算$\sqrt{(-4)^{2}}$;利用平方差公式和完全平方公式计算(1-$\sqrt{5}$)($\sqrt{5}$+1)+($\sqrt{5}$-1)2.
解答 解:$\sqrt{(-4)^{2}}$=|-4|=4;
(1-$\sqrt{5}$)($\sqrt{5}$+1)+($\sqrt{5}$-1)2=1-($\sqrt{5}$)2+($\sqrt{5}$)2-2$\sqrt{5}$+1=2-2$\sqrt{5}$.
故答案为4,2-2$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
6.已知等腰三角形的两边长分别为6厘米和3厘米,则该等腰三角形的周长是( )
| A. | 9厘米 | B. | 12厘米 | C. | 15厘米 | D. | 12厘米或15厘米 |
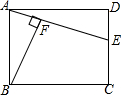 如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:BF•DE=AF•AD.
如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:BF•DE=AF•AD.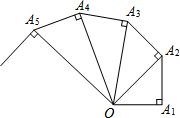 如图,OA1⊥A1A2,OA2⊥A2A3,OA3⊥A3A4…,OA1=A1A2=A2A3=…=1,则OA10=$\sqrt{10}$.
如图,OA1⊥A1A2,OA2⊥A2A3,OA3⊥A3A4…,OA1=A1A2=A2A3=…=1,则OA10=$\sqrt{10}$. 如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.
如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.