题目内容
5．
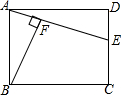如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：BF•DE=AF•AD．
分析 根据四边形ABCD是矩形可得出∠BAD=∠D=90°，再根据相似三角形的判定定理可得出△ADE∽△BFA，由相似三角形的对应边成比例即可得出结论．
解答 证明：∵四边形ABCD是矩形，
∴∠BAD=∠D=90°，
∴∠1+∠2=90°，
∵BF⊥AE，
∴∠AFB=∠1+∠3=90°，
∴∠2=∠3，
又∵∠D=∠AFB=90°，
∴△ADE∽△BFA．
∴$\frac{AD}{BF}=\frac{DE}{AF}$，
∴BF•DE=AF•AD．
点评 本题考查的是相似三角形的判定与性质，能根据题意得出△ADE∽△BFA是解答此题的关键．
练习册系列答案
相关题目
13．下列各式中，正确的是（ ）
| A． | $\sqrt{（-5{）^2}}$=-5 | B． | -$\sqrt{5^2}$=-5 | C． | $\sqrt{（±5{）^2}}$=±5 | D． | $\sqrt{5^2}$=±5 |
