题目内容
17．
如图，△ABC中，EF∥BC，PG∥AB，AP=CF，求证：△AEF≌△PGC．
分析 根据全等三角形的判定证明即可．
解答 证明：∵EF∥BC，PG∥AB，
∴∠C=∠AFE，∠GPC=∠A，
又AP=CF，
∴AP+PF=CF+PF，
∴AF=PC，
∴由$\left\{\begin{array}{l}∠A=∠GPC\\∠AFE=∠C\\ AF=PC\end{array}\right.$，得△AEF≌△PGC．
点评 本题考查了平行线的性质和全等三角形的应用，关键是推出证两三角形全等的三个条件，题目比较典型，难度不大．
练习册系列答案
相关题目
如图，已知∠BDC=∠CEB=90°，BE、CD交于点O，且AO平分∠BAC，求证：OB=OC．
8．
如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，A2017的横坐标为（ ）
如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，A2017的横坐标为（ ）| A． | 1010 | B． | 2 | C． | 1 | D． | -1006 |
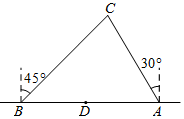如图，两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍船只停在C处海域，AB=60（$\sqrt{3}$+1）海里，在B处测得C在北偏东45°反向上，A处测得C在北偏西30°方向上，在海岸线AB上有一灯塔D，测得AD=100海里．
12．
如图，在平行四边形ABCD中，AE平分∠DAB，∠AED=26°，则∠C的度数为（ ）
如图，在平行四边形ABCD中，AE平分∠DAB，∠AED=26°，则∠C的度数为（ ）| A． | 26° | B． | 42° | C． | 52° | D． | 56° |
7．下列各运算中，计算正确的是（ ）
| A． | a0=1 | B． | $\sqrt{32}$-$\sqrt{8}$=2$\sqrt{2}$ | C． | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D． | $\sqrt{18}$÷2=3 |