题目内容
2.阅读理解:有一个n位自然数$\overline{{n_1}{n_2}{n_3}…{n_n}}$(n,n1,n2,n3,…nn是正整数,n≥2,1≤n1,n2,n3,…nn<9),若交换不同数位上的数字得到一新数则叫这个n位自然数$\overline{{n_1}{n_2}{n_3}…{n_n}}$的一个“轮换数”,如:$\overline{{n_2}{n_1}{n_3}…{n_n}}$,$\overline{{n_1}{n_3}{n_2}…{n_n}}$均是$\overline{{n_1}{n_2}{n_3}…{n_n}}$的一个“轮换数”;36是63的一个“轮换数”,243是324的一个“轮换数”.(1)写出213的所有轮换数.
(2)证明:任何一个3位自然数$\overline{{n_1}{n_2}{n_3}}$与它所有轮换数的和是111的倍数.
(3)试求:4213与它所有轮换数的和.
分析 表示出这个三位自然数,和轮换三位自然数,得到能整除即可.
解答 (1)213的所有“轮换数”为:231,123,132,321,312,
(2)$\overline{{n_1}{n_2}{n_3}}$与它所有轮换数的和为:$\overline{{n_1}{n_2}{n_3}}$+$\overline{{n_1}{n_2}{n_3}}$+$\overline{{n_1}{n_2}{n_3}}$+$\overline{{n_1}{n_2}{n_3}}$+$\overline{{n_1}{n_2}{n_3}}$+$\overline{{n_1}{n_2}{n_3}}$,
=2($\overline{{n_1}{n_2}{n_3}}$).
=2($\overline{{n_1}{n_2}{n_3}}$)×111
$\overline{{n_1}{n_2}{n_3}}$是正整数$\overline{{n_1}{n_2}{n_3}}$是正整数
所以2($\overline{{n_1}{n_2}{n_3}}$)×111是111的倍数,即任何一个3位自然数$\overline{{n_1}{n_2}{n_3}}$与它所有轮换数的和是111的倍数;
(3)当4为首位时,由(1)知,213与213数位轮换共有6种情况,再由(2)运算过程可知,4213与它所有轮换数的和为:
6×(1+2+3+4)×1111=66660.
点评 此题是数的整除性,主要考查了3的倍数,4的倍数,5的倍数的特点,解本题的关键是用5的倍数求出b的值.

练习册系列答案
相关题目
10.a与$\frac{1}{2}$互为相反数,则a=( )
| A. | -2 | B. | 2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
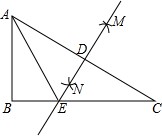 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN分别交AC、BC于点D、E,连结AE,若AB=3,AC=5,则BE的长为$\frac{7}{8}$.
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN分别交AC、BC于点D、E,连结AE,若AB=3,AC=5,则BE的长为$\frac{7}{8}$.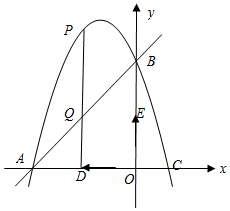 如图,抛物线经过点A(-3,0)、B(0,3),C(1,0).
如图,抛物线经过点A(-3,0)、B(0,3),C(1,0). 如图,△ABC中,EF∥BC,PG∥AB,AP=CF,
如图,△ABC中,EF∥BC,PG∥AB,AP=CF, 已知:如图,AD=BC,AC=BD.求证:∠OCD=∠ODC.
已知:如图,AD=BC,AC=BD.求证:∠OCD=∠ODC. 已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由.
已知,在四边形ABCD中,AB=AD,∠B=∠D,请说明CB=CD的理由. 如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°.
如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°. 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图: