如图.在平行四边形ABCD中.AE平分∠DAB.∠AED=26°.则∠C的度数为( )A．26°B．42°C．52°D．56° 题目和参考答案——青夏教育精英家教网—

题目内容

12．

如图，在平行四边形ABCD中，AE平分∠DAB，∠AED=26°，则∠C的度数为（　　）

A．

26°

B．

42°

C．

52°

D．

56°

分析由平行四边形的性质可求得∠EAB=∠AED，再结合角平分线的定义可求得∠DAB，再利用平行四边形的性质可求得答案．

解答解：
∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠DEA=∠BAE=26°，
∵AE平分∠DAB，
∴∠DAB=2∠BAE=52°，
∵四边形ABCD为平行四边形，
∴∠C=∠BAD=52°，
故选C．

点评本题主要考查平行四边形的性质，掌握平行四边形的对边平行、对角相等是解题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

2．

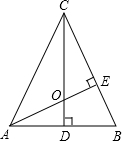如图，在△ABC中，AC=BC，AE⊥BC于E，CD⊥AB于D，AE与CD相交于点O，且AE=CE，求证：AD=$\frac{1}{2}$CO．

3．下列图形是轴对称图形但不是中心对称图形的是（　　）

20．计算：-3³+（-1）²⁰¹⁶÷$\frac{1}{6}$+（-5）²．

7．已知扇形的圆心角为150°，半径为6cm，则该扇形的侧面积为（　　）

17．

如图，△ABC中，EF∥BC，PG∥AB，AP=CF，
求证：△AEF≌△PGC．

4．正五边形ABCDE．
（1）若M，N分别是边DE，AE的中点，连接CM，DN，求证：$\frac{1}{2}$DE²=DP•DN：
（2）若O为边BD的中点，连接EO并延长交BC于点G．求$\frac{BG}{CG}$的值；
（3）若G为BC的中点．连接EG交BD于H．若AB=$\sqrt{5}$+1．直接写出BH的长

1．为了了解九年级学生参加体育活动的情况，某校对九年级部分学生进行问卷调查，其中一个问题是“你平均每天参加体育活动的时间是多少？”共有4个选项：
A．1.5h以上 B.1-1.5h C.0.5-1h D.0.5h以下（这里的1-1.5表示大于或等于1同时小于1.5，本题类似的记号均表示这一含义），根据调查结果绘制了如下两幅不完幅的统计图．

请你根据以上信息，解答下列问题：
（1）本次调查采用的调查方式是抽样调查；共调查了学生40名．
（2）请补全条形统计图和扇形统计图．
（3）若该校有500名九年级学生，估计该校九年级有多少名学生平均每天参加体育活动的时间至少1h．

2．

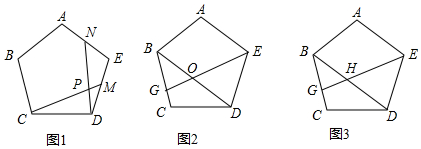
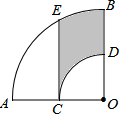如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交弧AB于点E，以点O为圆心，OC的长为半径作弧CD交OB于点D，若OA=4，则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$．

试题分类