题目内容
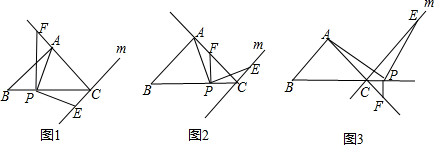
6.如图1,在△ABC中,AB=AC,AC⊥AB,过点C作AB的平行线m,取直线BC上一点P,连接AP,过P作AP的垂线,交直线m于点E,再过点P作BC的垂线,交直线AC于点F(1)如图1,点F在线段CA的延长线上时,求证:CF-CE=AC;
(2)如图2,点F在线段CA的上时,AC、CE、CF三条线段的数量关系为CF+CE=AC;
(3)如图3,点F在线段AC的延长线上时,AC、CE、CF三条线段有怎样的数量关系?并证明.
分析 (1)由图象可知CF-AF=AC,要证明CF-CE=AC,只要证明利用全等三角形证明AF=CE即可.
(2)结论:CF+CE=AC,由图象可知CF+AF=AC,要证明CF+CE=AC,只要证明AF=CE即可.
(3)结论:CE-CF=AC,由图象可知AF-CF=AC,要证明CE-CF=AC.只要证明CE=AF即可.
解答 (1)证明:如图1中,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵AC⊥EC,
∴∠ACE=90°,
∴∠PCE=90°-∠ACB=45°,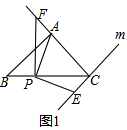
∵FP⊥PC,
∴∠FPC=90°,
∴∠PFC=90°-∠FCP=45°,
∴∠PFC=∠PCF=45°,
∴PF=PC,
∵AP⊥PE,
∴∠APE=90°,
∴∠FPC=∠APE=90°,
∴∠FPA=∠CPE,
在△FPA和△CPE中,
$\left\{\begin{array}{l}{∠PFA=∠PCE}\\{PF=PC}\\{∠FPA=∠CPE}\end{array}\right.$,
∴△FPA≌△CPE,
∴AF=CE,
∴CF-CE=CF-AF=AC.
(2)如图2中,结论:CF+CE=AC,理由如下:
解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵AC⊥EC,
∴∠ACE=90°,
∴∠PCE=90°+∠ACB=135°
∵FP⊥PC,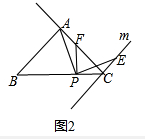
∴∠FPC=90°,
∴∠PFC=90°-∠FCP=45°,
∠PFC=∠PCF=45°,
∴PF=PC,∠AFP=180°-∠PFC=135°=∠PCE,
∵AP⊥PE,
∴∠APE=90°,
∴∠FPC=∠APE=90°,
∴∠FPA=∠CPE
在△FPA和△CPE中,
$\left\{\begin{array}{l}{∠PFA=∠PCE}\\{PF=PC}\\{∠FPA=∠CPE}\end{array}\right.$,
∴△FPA≌△CPE,
∴AF=CE,
∴CF+CE=CF+AF=AC.
故答案为CF+CE=AC.
(3)如图3中,结论:CE-CF=AC,理由如下:
证明:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=∠PCF=45°,
∵AC⊥EC,
∴∠ACE=90°,
∴∠PCE=180°-∠ACB-∠ACE=45°
∵FP⊥PC
∴∠FPC=90°,
∴∠PFC=90°-∠FCP=45°,
∠PFC=∠PCF=45°,
∴PF=PC,∠AFP=∠PCE,
∵AP⊥PE,
∴∠APE=90°,
∴∠FPC=∠APE=90°,
∴∠FPA=∠CPE
在△FPA和△CPE中,
$\left\{\begin{array}{l}{∠PFA=∠PCE}\\{PF=PC}\\{∠FPA=∠CPE}\end{array}\right.$,
∴△FPA≌△CPE,
∴AF=CE,
∴EC-CF=AF-CF=AC.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质,解题的关键是正确寻找全等三角形,考查了学生的认识图形的能力,这类题目有个共同特征形变一些结论基本不变.

| A. | x2=1 | B. | x+$\frac{1}{x}$=1 | C. | x+2y=1 | D. | x(x-1)=x2 |
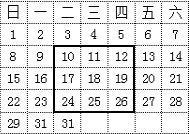 如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).
如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).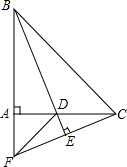 已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.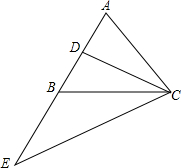 已知△ABC,AB=AC,AD=BD,AB=BE,求证:∠ACD=∠E.
已知△ABC,AB=AC,AD=BD,AB=BE,求证:∠ACD=∠E.