题目内容
10.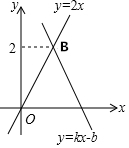 如图,函数y=kx+b(k≠0)的图象与函数y=2x的图象交于点B,则不等式kx+b≤2x的解集为( )
如图,函数y=kx+b(k≠0)的图象与函数y=2x的图象交于点B,则不等式kx+b≤2x的解集为( )| A. | x≥0 | B. | x≤1 | C. | x≥1 | D. | x≥2 |
分析 先利用正比例函数解析式确定B点坐标,然后利用函数图象,找出函数y=2x的图象不在直线y=kx+b的下方所对应的自变量的范围即可.
解答 解:当y=2时,2x=2,解得x=1,则B(1,2),
当x≥1时,kx+b≤2x.
故选C.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
20.将分式$\frac{6m{n}^{3}}{4{m}^{3}n}$化成最简分式的结果正确的是( )
| A. | $\frac{6{n}^{2}}{4{m}^{2}}$ | B. | $\frac{6n}{4m}$ | C. | $\frac{3{n}^{2}}{2{m}^{2}}$ | D. | $\frac{3n}{2m}$ |
18.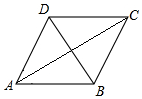 如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
 如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )
如图,菱形ABCD的边长为20,∠DAB=60,对角线为AC和BD,那么菱形的面积为( )| A. | 50$\sqrt{3}$ | B. | 100$\sqrt{3}$ | C. | 200$\sqrt{3}$ | D. | 400$\sqrt{3}$ |
2.五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价-进价)
19.为了解某小区居民的日用电情况,居住在小区的一名同学随机抽查了15户家庭的日用电量,具体结果如下表所示:
则关于这15户家庭的日用电量,下列说法正确的是( )
| 日用电量/度 | 5 | 6 | 7 | 8 | 10 |
| 户数 | 2 | 5 | 4 | 3 | l |
| A. | 众数是10度 | B. | 平均数是7度 | C. | 中位数是6度 | D. | 中位数是7度 |
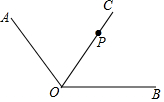 如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).
如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).