题目内容
6．
如图，∠1=∠2，则下列结论一定成立的是（ ）| A． | ∠B=∠D | B． | ∠3=∠4 | C． | ∠D+∠BCD=180° | D． | ∠D+∠BAD=180° |
分析 先根据平行线的判定由∠1=∠2得到AD∥CD，然后根据平行线的性质对各选项进行判断．
解答 解：∵∠1=∠2，
∴AD∥CD，
∴∠D+∠BCD=180°．
故选C．
点评 本题考查了平行线的判定与性质：平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
16．
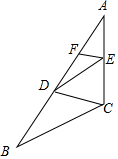如图，△ABC中，点D、F在边AB上，点E在边AC上，如果DE∥BC，EF∥CD，那么一定有（ ）
如图，△ABC中，点D、F在边AB上，点E在边AC上，如果DE∥BC，EF∥CD，那么一定有（ ）| A． | DE2=AD•AE | B． | AD2=AF•AB | C． | AE2=AF•AD | D． | AD2=AE•AC |
14．某校计划购进A、B两种花卉，两次购进的花卉的数量与每次总费用如表所示：
（1）你从表格中获取了什么信息？请用自己的简练言，写出一条．这条信息为：购买A种花卉10株和B种花卉25株共花费225元
（2）求A、B两种花卉每株的价格分别是多少元？
| 花卉数量（株） | 总费用（元） | ||
| A | B | ||
| 第1次购买 | 10 | 25 | 225 |
| 第2次购买 | 20 | 15 | 275 |
（2）求A、B两种花卉每株的价格分别是多少元？
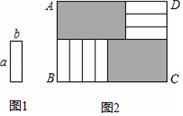七张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影部分，设左上角与右下角的阴影部分的面积的差为S=S1-S2，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足的关系式是a=3b．
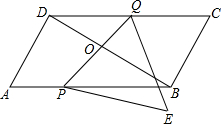如图，在?ABCD中，O是对角线BD的中点，AD⊥BD，AB=4cm，∠BAD=60°，动点P从点A出发，以2cm/s的速度沿折线AB-BC向终点C运动，连结PO并延长交折线CD-DA于点Q，将线段PQ绕着点P顺时针旋转60°得到线段PE，连结QE，设点P的运动时间为t（s）
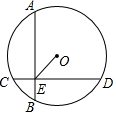如图，⊙O的直径为10，两条弦AB⊥CD，垂足为E，且AB=CD=8，则OE=3$\sqrt{2}$．
16．在平面直角坐标系xOy中，已知A（2，3），B（1，0），C是y轴上的一个动点，当△ABC的周长最小时，则△ABC的面积为（ ）
| A． | 2 | B． | $\frac{2}{3}$ | C． | 3$\sqrt{2}$+$\sqrt{10}$ | D． | $\frac{4}{3}$ |