题目内容
18.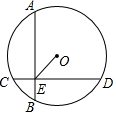 如图,⊙O的直径为10,两条弦AB⊥CD,垂足为E,且AB=CD=8,则OE=3$\sqrt{2}$.
如图,⊙O的直径为10,两条弦AB⊥CD,垂足为E,且AB=CD=8,则OE=3$\sqrt{2}$.
分析 直接利用垂径定理结合勾股定理得出ON,OM的长,再利用矩形的判定与性质得出EM的长,再利用勾股定理得出答案.
解答 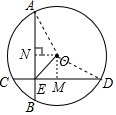 解:过点O作ON⊥AB于点N,过点O作OM⊥CD于点M,连接AO,OD,
解:过点O作ON⊥AB于点N,过点O作OM⊥CD于点M,连接AO,OD,
∵⊙O的直径为10,
∴AO=DO=5,
∵AB=CD=8,ON⊥AB,OM⊥DC,
∴AN=DM=4,
∴ON=OM=$\sqrt{{5}^{2}-{4}^{2}}$=3,
由题意可得:∠ONE=∠AED=∠OME=90°,
∴四边形ONEM是矩形,
∴EM=ON=3,
∴EO=$\sqrt{O{M}^{2}+E{M}^{2}}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 此题主要考查了垂径定理以及勾股定理、矩形的判定与性质等知识,正确得出O到AB,CD的距离是解题关键.

练习册系列答案
相关题目
7.下列各式由左边到右边的变形中,属于因式分解的是( )
| A. | x2-2x+2=x(x-2)+2 | B. | (x+y)(x-y)=x2-y2 | ||
| C. | (2a-b)2=4a2-4ab+b2 | D. | x2+4x+4=(x+2)2 |
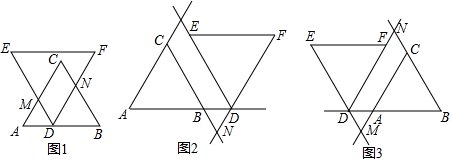
6. 如图,∠1=∠2,则下列结论一定成立的是( )
如图,∠1=∠2,则下列结论一定成立的是( )
 如图,∠1=∠2,则下列结论一定成立的是( )
如图,∠1=∠2,则下列结论一定成立的是( )| A. | ∠B=∠D | B. | ∠3=∠4 | C. | ∠D+∠BCD=180° | D. | ∠D+∠BAD=180° |
10.从1、3、5、7、9中任取两个数字,组成的两位数是奇数,这是( )
| A. | 必然事件 | B. | 随机事件 | ||
| C. | 不可能事件 | D. | 何类事件不能确定 |
7.不等式组$\left\{\begin{array}{l}{1-x≥0}\\{2x-1>-3}\end{array}\right.$的整数解是( )
| A. | -1,0 | B. | -1,1 | C. | 0,1 | D. | -1,0,1 |
8.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | 2.2020020002 | C. | $\root{3}{9}$ | D. | -1 |
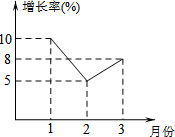 某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长,其中正确的结论序号是①③.
某市统计局统计了今年第一季度每月人均GDP的增长情况,并绘制了如图所示的统计图,下列结论:①1月份的人均GDP增长率最高;②2月份的人均GDP比1月份低;③这三个月的人均GDP都在增长,其中正确的结论序号是①③. 已知抛物线L1:y1=x2+6x+5k和抛物线L2:y2=kx2+6kx+5k,其中k≠0.
已知抛物线L1:y1=x2+6x+5k和抛物线L2:y2=kx2+6kx+5k,其中k≠0.