题目内容
16．已知关于x的方程x2+2x=m-1无实根，试说明x2+mx=1-2m必有两个不相等的实数根的理由．分析 由方程x2+2x=m-1无实根可得m＜0，再判断方程x2+mx+2m-1=0中，△=m2-4（2m-1）=m2-8m+16-12=（m-4）2-12值的情况即可．
解答 解：∵方程x2+2x=m-1，即x2+2x+1=m无实根，
∴（x+1）2=m无实数根，
∴m＜0，
则方程x2+mx+2m-1=0中，
△=m2-4（2m-1）=m2-8m+16-12=（m-4）2-12，
∵m＜0，
∴m-4＜-4，
则（m-4）2＞16，
∴（m-4）2-12＞4，
故方程有两个不相等的实数根．
点评 本题主要考查方程的根的判别式，熟练掌握一元二次方程根的判别式与根的个数间的关系是解题的关键．
练习册系列答案
相关题目
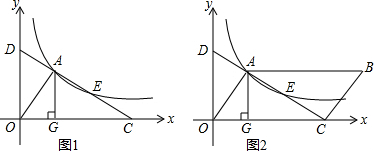
如图ABC中，AB=AC，⊙O为△ABC的外接围，D为⊙O外一点，∠DCA=∠ACB．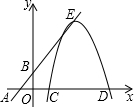
如图，一次函数y=x+2与x轴交于点A，与y轴交于点B，一抛物线的顶点在直线AB上，形状与函数y=-$\frac{1}{2}$x2图象相同，它与x轴分别交于点C、D（点C在点D的左侧），抛物线的顶点为点E．