题目内容
15．一道斜坡的坡比为1：$\sqrt{5}$，若坡高为$\sqrt{3}$，则斜坡长为3$\sqrt{2}$．分析 根据坡度的概念求出斜坡的水平宽度，再根据勾股定理求出斜边长．
解答 
解：如图，由题意得：AC：BC=1：$\sqrt{5}$，
又∵AC=$\sqrt{3}$，
∴BC=$\sqrt{15}$，
由勾股定理得，AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{2}$．
故答案为：3$\sqrt{2}$．
点评 此题主要考查解直角三角形的应用-坡度坡角问题，以及勾股定理，正确求得BC的长是解题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
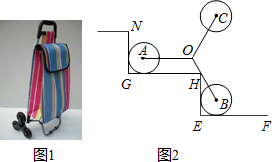如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图，定长的轮架杆OA，OB，OC抽象为线段，有OA=OB=OC，且∠AOB=120°．折线NG-GH-HE-EF表示楼梯，GH，EF是水平线，NG，HE是铅垂线，半径相等的小轮子⊙A，⊙B与楼梯两边都相切，且AO∥GH．如图2，若点H在线段OB时，则$\frac{BH}{OH}$的值是$\sqrt{3}$．
如图，直线AB与CD相交于点O，OD恰为∠BOE的角平分线．
如图，请你求出阴影部分的面积（用含有x的代数式表示）．
如图所示，OM平分∠BOC，ON平分∠AOC，