题目内容
一次函数y=k1x+b和反比例函数y=
的图象相交于点P(m-1,n+1),点Q(0,a)在函数y=k1x+b的图象上,且m,n是关于x的方程ax2-(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),求一次函数和反比例函数的解析式.
| k2 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:m,n是关于x的方程ax2-(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),得出a=-1,m=2,n=0,或m=0,n=2,从而求得P、Q的坐标,根据待定系数法即可求得一次函数和反比例函数的解析式.
解答:解:解方程ax2-(3a+1)x+2(a+1)=0,
得:x=2,x=
∵m,n是关于x的方程ax2-(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),
∴a=-1,
∴x1=2,x2=0,
∴m=2,n=0,或m=0,n=2,
∴P(1,1),或P(-1,3),Q(0,-1),
把P,Q的坐标代入y=k1x+b得
或
,
解得
或
,
∴一次函数的解析式为y=2x-1或y=-4x-1;
把P的坐标代入y=
得k2=1或-3,
∴反比例函数的解析式y=
或y=-
.
得:x=2,x=
| a+1 |
| a |
∵m,n是关于x的方程ax2-(3a+1)x+2(a+1)=0的两个不相等的整数根(其中a为整数),
∴a=-1,
∴x1=2,x2=0,
∴m=2,n=0,或m=0,n=2,
∴P(1,1),或P(-1,3),Q(0,-1),
把P,Q的坐标代入y=k1x+b得
|
|
解得
|
|
∴一次函数的解析式为y=2x-1或y=-4x-1;
把P的坐标代入y=
| k2 |
| x |
∴反比例函数的解析式y=
| 1 |
| x |
| 3 |
| x |
点评:本题考查了方程的解,反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,已知AB=AC,EB=EC,AE的延长线交BC于点D,求证:BD=CD.
如图,已知AB=AC,EB=EC,AE的延长线交BC于点D,求证:BD=CD. 已知有理数a、b在数轴上对应的位置如图所示,化简|2-3b|-2|2+b|+|a-2|+3|3b-2a|.
已知有理数a、b在数轴上对应的位置如图所示,化简|2-3b|-2|2+b|+|a-2|+3|3b-2a|.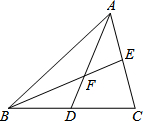 如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?