题目内容
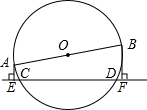 如图,AB是⊙O直径,CD是弦.若AB=85,CD=75,那么A、B两点到直线CD的距离之和为
如图,AB是⊙O直径,CD是弦.若AB=85,CD=75,那么A、B两点到直线CD的距离之和为考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:过OM⊥DC于M,求出OM为梯形中位线,求出AE+BF=2OM,根据垂径定理求出DM=
CD=37.5,求出OD,根据勾股定理求出OM即可.
| 1 |
| 2 |
解答: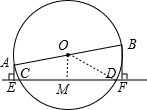
解:过OM⊥DC于M,
∵AE⊥EF,BF⊥EF,
∴AE∥OM∥BF,
∵OA=OB,
∴EM=FM,
∴OM=
(AE+BF),
∴AE+BF=2OM,
∵AB=85,
∴AO=OD=
=42.5,
∵CD=75,OM⊥CD,
∴DM=
CD=
=37.5,
在Rt△ODM中,由勾股定理得:OM=
=
=20,
∴AE+BF=2×20=40,
故答案为:40.

解:过OM⊥DC于M,
∵AE⊥EF,BF⊥EF,
∴AE∥OM∥BF,
∵OA=OB,
∴EM=FM,
∴OM=
| 1 |
| 2 |
∴AE+BF=2OM,
∵AB=85,
∴AO=OD=
| 85 |
| 2 |
∵CD=75,OM⊥CD,
∴DM=
| 1 |
| 2 |
| 75 |
| 2 |
在Rt△ODM中,由勾股定理得:OM=
| OD2-DM2 |
| 42.52-37.52 |
∴AE+BF=2×20=40,
故答案为:40.
点评:本题考查了勾股定理,垂径定理,梯形的中位线的应用,解此题的关键是求出OM的长和求出AE+BF=2OM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆内接四边形ABCD中,∠A:∠B:∠C:∠D可以是( )
| A、5:2:3:4 |
| B、5:3:2:4 |
| C、2:4:3:5 |
| D、4:2:5:3 |
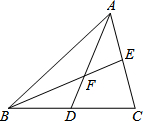 如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
如图,△ABC的中线AD、BE相交于点F.△ABF与四边形CEFD的面积有怎样的数量关系?为什么?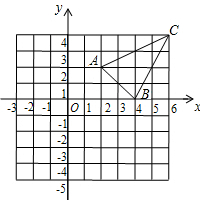 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4)以原点为位似中心,将△ABC缩小,位似比为1:2,则线段AC中点P变换后对应点的坐标为 如图所示,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立平面直角坐标系,回答下列问题:
如图所示,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立平面直角坐标系,回答下列问题: