题目内容
14.某校运动会需购买A、B两种奖品共100件.若A种奖品每件10元,B种奖品每件15元,设购买A、B两种奖品的总费用为W元,购买A种奖品m件.(1)求出W(元)与m(件)之间的函数关系式;
(2)若总费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,试求出最少费用W的值.
分析 (1)根据总费用=A、B两种奖品费用的和,即可解决问题.
(2)列出不等式组,解不等式组即可.
解答 解:(1)由题意W=10m+15(100-m)=-5m+1500.
(2)由$\left\{\begin{array}{l}{-5m+1500≤1150\\;}\\{m≤3(100-m)}\end{array}\right.$解得70≤m≤75,
∵W=-5m+1500,
k=-5<0,W随m的增大而减小,
∴当m=75时,W最小值=1500-5×75=1125(元).
点评 本题考查一次函数的应用,一元一次不等式组等知识,解题的关键是学会构建一次函数,利用一次函数的性质解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
| A. | 2$\sqrt{3}$cm | B. | 4$\sqrt{3}$cm | C. | 6$\sqrt{3}$cm | D. | 8$\sqrt{3}$cm |
19.如果方程2xm-1-3y2m+n=1是关于x、y的二元一次方程,那么m、n的值分别为( )
| A. | 1,0 | B. | 2,-3 | C. | 1,-3 | D. | 1,1 |
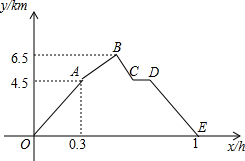 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.