题目内容
16.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为m>0?分析 直接利用顶点形式得出顶点坐标,结合第一象限点的特点列出不等式组解答即可.
解答 解:∵抛物线y=(x-m)2+(m+1),
∴顶点坐标为(m,m+1),
∵顶点在第一象限,
∴m>0,m+1>0,
∴m的取值范围为m>0.
故答案为:m>0.
点评 此题考查二次函数的性质,二次函数y=a(x-h)2+k的顶点坐标为(h,k),以及各个象限点的坐标特征.

练习册系列答案
相关题目
6.已知(m2-4)x2-(m+2)x+8=0是关于未知数x的一元一次方程,求代数式-199(m+x)(m-2x)+m的值( )
| A. | 1592 | B. | 1593 | C. | 1594 | D. | 1595 |
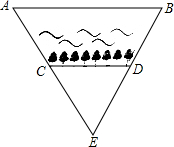 某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.
某市护城河的某段是笔直的,在护城河的北岸边每隔35米就有一个垃圾箱,在护城河的南岸边每隔3米就有一棵树,张萌站在离南岸18米的点E处看北岸,发观北岸相邻的两个垃圾箱A,B恰好被南岸的两棵树C、D遮住,并且这两棵树之间还有6棵树.