题目内容
12.某校开展“人人读书”活动.小明为调查同学们的阅读兴趣,抽样调查了40名学生在本校图书馆的借阅情况(每人每次只能借阅一本图书),绘制了统计图1.并根据图书馆各类图书所占比例情况绘制了统计图2,已知综合类图书有40本.校图书馆各类图书所占比例统计图各类图书借阅人次分布统计图
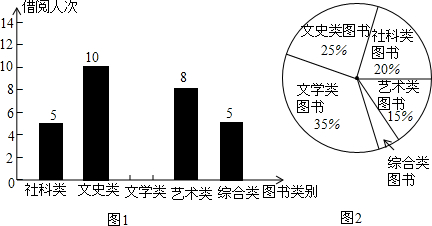
(1)补全统计图1;
(2)该校图书馆共有图书800本;
(3)若该校共有学生1000人,试估算,借阅文学类图书的有350人.
分析 (1)根据有理数的减法,可得文学类借阅人次,根据文学借阅人次,可得答案;
(2)根据各类数借阅的人次除以借阅数所占该类书的比例,可得该类书的数量,根据有理数的加法,可得答案;
(4)根据学校总人数乘以文学类借阅人次所占的百分比,可得答案.
解答 解:(1)文学类借阅人次40-5-10-8-5=12(人).
补全统计图为:
(2)5÷20%+10÷25%+12÷35%+8÷15%5÷5%=800(本).
(3)1000×35%=350(人).
故答案为:800;350.
点评 本题考查了条形统计图,观察统计图获得有效信息是解题关键,利用样本估计总体.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.计算(2x-3y)2的结果正确的是( )
| A. | 4x2-9y2 | B. | 2x2+4xy+9y2 | C. | 4x2-6xy+9y2 | D. | 4x2-12xy+9y2 |
1.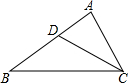 如图所示,要使得△ABC∽△ACD,只需增加条件( )
如图所示,要使得△ABC∽△ACD,只需增加条件( )
 如图所示,要使得△ABC∽△ACD,只需增加条件( )
如图所示,要使得△ABC∽△ACD,只需增加条件( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | CD2=AD•DB | C. | ∠B=∠BCD | D. | ∠ADC=∠ACB |
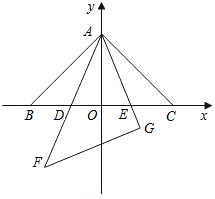 如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论:
如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论:
 如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.
如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.