题目内容
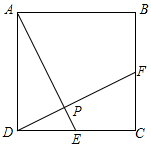 正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.
正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.(1)求证:AE=DF;
(2)若PA=4,tan∠FDC=
| 1 |
| 2 |
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)证明△ADE≌△DCF,得到AE=DF,即可解决问题.
(2)证明tan∠DAE=tan∠FDC=
,结合tan∠DAE=
,得到AD=2DE(设为2λ);证明AE=
λ;由射影定理得AD2=AP•AE,即4λ2=4×
λ,解得λ=
即可解决问题.
(2)证明tan∠DAE=tan∠FDC=
| 1 |
| 2 |
| DE |
| AD |
| 5 |
| 5 |
| 5 |
解答: (1)证明:如图,∵四边形ABCD为正方形,
(1)证明:如图,∵四边形ABCD为正方形,
∴∠ADE=∠DCF=90°,AD=DC;而AE⊥DF,
∴∠DAE+∠AED=∠AED+∠FDC,
∴∠DAE=∠FDC;
在△ADE与△DCF中,
,
∴△ADE≌△DCF(ASA),
∴AE=DF.
(2)解:∵∠DAE=∠FDC,
∴tan∠DAE=tan∠FDC=
,而tan∠DAE=
,
∴AD=2DE(设为2λ);
由勾股定理得:AE=
λ;
由射影定理得:AD2=AP•AE,
即4λ2=4×
λ,解得:λ=
,
∴AD=2
.
 (1)证明:如图,∵四边形ABCD为正方形,
(1)证明:如图,∵四边形ABCD为正方形,∴∠ADE=∠DCF=90°,AD=DC;而AE⊥DF,
∴∠DAE+∠AED=∠AED+∠FDC,
∴∠DAE=∠FDC;
在△ADE与△DCF中,
|
∴△ADE≌△DCF(ASA),
∴AE=DF.
(2)解:∵∠DAE=∠FDC,
∴tan∠DAE=tan∠FDC=
| 1 |
| 2 |
| DE |
| AD |
∴AD=2DE(设为2λ);
由勾股定理得:AE=
| 5 |
由射影定理得:AD2=AP•AE,
即4λ2=4×
| 5 |
| 5 |
∴AD=2
| 5 |
点评:该题主要考查了全等三角形的判定及其性质、勾股定理、射影定理等几何知识点及其应用问题;解题的关键是牢固掌握全等三角形的判定及其性质等几何知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOD=70°,则∠BOD的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOD=70°,则∠BOD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |

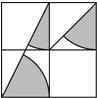 如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).
如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).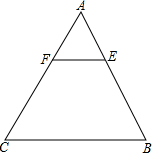 如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.
如图,在△ABC中,AE:EB=1;2,EF∥BC,求S△AEF:S△ABC的值.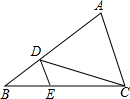 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=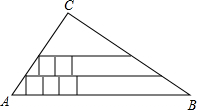 如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放
如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放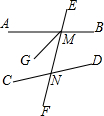 如图,图中同位角一共
如图,图中同位角一共