题目内容
 如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据对顶角、邻补角,可得∠BOD、∠AOD,根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案.
(2)根据角平分线的性质,可得∠DOF与∠DOE的度数,根据角的和差,可得答案.
解答:解:(1)由对顶角相等,得∠BOD=∠AOC=50°,
由OF平分∠BOD,得∠DOF=
∠BOD=
×50°=25°,
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=
∠AOD=
×130°=65°,
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数变化,
由OF平分∠BOD,得∠DOF=
∠BOD,
由OE平分∠AOD,得∠DOE=
∠AOD,
由角的和差,得∠EOF=∠DOF+∠DOE
=
∠BOD+
∠AOD
=
(∠AOD+∠BOD)
=
∠AOB=90°.
由OF平分∠BOD,得∠DOF=
| 1 |
| 2 |
| 1 |
| 2 |
由邻补角互补,得∠AOD=180°-∠AOC=180°-50°=130°,
由OE平分∠AOD,得∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠EOF=∠DOF+∠DOE=25°+65°=90°;
(2)∠AOC的度数变化时,∠EOF的度数变化,
由OF平分∠BOD,得∠DOF=
| 1 |
| 2 |
由OE平分∠AOD,得∠DOE=
| 1 |
| 2 |
由角的和差,得∠EOF=∠DOF+∠DOE
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查了对顶角、邻补角,利用了对顶角的性质,邻补角的定义,角平分线的性质,角的和差.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
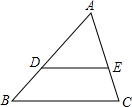 如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )
如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,将半圆O绕直径的端点B逆时针旋转30°,得到半圆O′,
如图,将半圆O绕直径的端点B逆时针旋转30°,得到半圆O′,
 如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B.
如图,已知A(3,0)、B(0,4),以A为顶点的抛物线与y轴交于点B. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,联结DE,F为线段DE上一点,且∠AFE=∠B.若AB=5,AD=8,AE=4,则AF的长为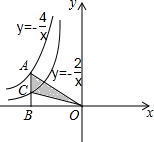 已知,如图,点A在反比例函数y=-
已知,如图,点A在反比例函数y=-