题目内容
3. 如图,△ABC中,CD⊥AB于D,E是AC的中点,∠B=45°,若AD=6,DE=5,则BC的长等于8$\sqrt{2}$.
如图,△ABC中,CD⊥AB于D,E是AC的中点,∠B=45°,若AD=6,DE=5,则BC的长等于8$\sqrt{2}$.
分析 由CD⊥AB于D,E是AC的中点,求得AC=2DE=10,利用勾股定理得出CD,进一步利用等腰直角三角形的性质和勾股定理求得答案即可.
解答 解:∵CD⊥AB于D,E是AC的中点,DE=5,
∴AC=2DE=10,
∴DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=8,
∵∠B=45°,
∴BD=CD=8,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$8\sqrt{2}$.
故答案为:8$\sqrt{2}$.
点评 此题考查勾股定理的实际运用,直角三角形斜边上的中线等于斜边的一半,以及等腰直角三角形的性质.

练习册系列答案
相关题目
14. 如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )
如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )
 如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )
如图,点O在直线AC上,BO⊥DO于点O,若∠1=145°,则∠3的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
15.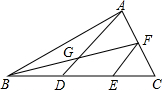 如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )
如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )
 如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )
如图,在△ABC中,D,E是BC边上的三等分点,F是AC边上的中点,AD与BF交于点G,则S△AGF:S△FEC为( )| A. | 1:1 | B. | 3:2 | C. | 9:4 | D. | 4:3 |
 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和3,则正方形的面积是10.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和3,则正方形的面积是10. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P在AC边上,点M、N在AB边上,(点M在点N的左侧),PM=PN,且∠MPN=∠A,连接CN.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P在AC边上,点M、N在AB边上,(点M在点N的左侧),PM=PN,且∠MPN=∠A,连接CN. 如图,∠C=30°,PA⊥OA于A,PB⊥OB于B,PA=2,PB=11,求OP的长.
如图,∠C=30°,PA⊥OA于A,PB⊥OB于B,PA=2,PB=11,求OP的长. 如图,是一个小正方形边长为1的8×8的网格,请你在网格中画出一个面积为6的
如图,是一个小正方形边长为1的8×8的网格,请你在网格中画出一个面积为6的