Question

15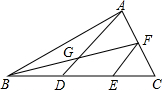．如图，在△ABC中，D，E是BC边上的三等分点，F是AC边上的中点，AD与BF交于点G，则S_△AGF：S_△FEC为（　　）

• A． 1：1
• B． 3：2
• C． 9：4
• D． 4：3

Answer 1

分析 根据三角形相似的性质以及等高的三角形面积比等于底的比，推导出S_△AGF和S_△FEC与S_△ABC的数量关系，即可求解．

解答 解：∵D，E是BC边上的三等分点，F是AC边上的中点，
∴AD∥EF，
∵D是BE的中点，
∴BG=FG，
∴S_△AGF=S_△FEC=$\frac{1}{2}$S_△ABF，
∵F是AC边上的中点，
∴S_△ABF=$\frac{1}{2}$S_△ABC，
∴S_△AGF=$\frac{1}{4}$S_△ABC，
∵F是AC边上的中点，AD∥EF，
∴$\frac{EF}{AD}=\frac{1}{2}$，
∴$\frac{S△FEC}{S△ADC}=\frac{1}{4}$，
∵D，E是BC边上的三等分点，
∴S_△ADC=$\frac{2}{3}$S_△ABC，
∴S_△FEC=$\frac{1}{6}$S_△ABC，
∴S_△AGF：S_△FEC=$\frac{1}{4}$S_△ABC：$\frac{1}{6}$S_△ABC=3：2．
故选：B．

点评 本题主要考查了相似三角形的判定与性质、三角形的中位线以及等高的三角形面积关系，找出S_△AGF和S_△FEC与S_△ABC的数量关系是本题的关键．