题目内容
1．一元二次方程kx2-（k+2）x-3=0的根的判别式为8，则k的值为-8+2$\sqrt{17}$或-8-2$\sqrt{17}$．分析 由题意可得△=（k+2）2-4k×（-3）=8，解此方程即可求得k的数值．
解答 解：∵一元二次方程kx2-（k+2）x-3=0的根的判别式为8，
∴△=（k+2）2-4k×（-3）=8，
即k2+16k-4=0，
解得：k1=-8+2$\sqrt{17}$，k2=-8-2$\sqrt{17}$．
故答案为：-8+2$\sqrt{17}$或-8-2$\sqrt{17}$．
点评 此题考查了一元二次方程根的判别式与一元二次方程的解法．解题的关键是掌握一元二次方程根的判别式为：△=b2-4ac．
练习册系列答案
阅读快车系列答案
相关题目
11．在△ABC中，∠A=100°，∠B=30°，则∠C为（ ）
| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
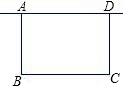如图，学校准备利用图书馆后面的场地用围栏圈建一个面积为60平方米的长方形ABCD，车棚的一边利用图书馆的后墙，墙长为a．
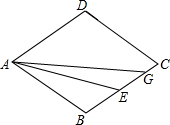如图，在菱形ABCD中，点E为BC的中点，点G在BC边上，连结AE，AG．
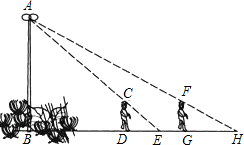如图，花丛中一根灯杆AB上有一盏路灯A，灯光下，小明在D点处的影长DE=3米，沿BD方向走到点G，DG=5米，这时小明的影长GH=4米，如果小明的身高为1.7米，求路灯A离地面的高度．
如图，AB⊥DB，CD⊥DB，∠1=∠2．射线BE与DF是否平行？请说明理由．