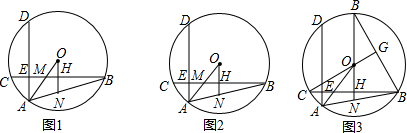
题目内容
13.在平行四边形ABCD中,对角线AC和BD交于点O,AC=8.(1)如图1,若AB⊥AC,BD=12,点P是线段AD上的动点(不包含端点A,D),过点P作PE⊥AC,垂足为点E,PF⊥BD,垂足为点F,设PE=x,PF=y,求y与x的函数关系式并直接写出自变量x的取值范围;
(2)如图2,若AE平分∠BAC,点F为BC中点,且点F保持在点E的右边,求线段BC的变化范围.
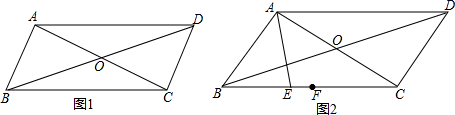
分析 (1)如图1,由平行四边形的性质易得BO=DO=6,AO=CO=4,BC=AD,利用勾股定理可得AB的长,BC,AD的长,由三角形的面积公式可得,S△AOD=S△POA+S△POD=2x+3y=$4\sqrt{5}$,S△AOD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×\frac{1}{2}×2\sqrt{5}×8$=4$\sqrt{5}$,得x,y的关系式;
(2)法一:如图2,由AE平分∠BAC,点F为BC中点,可得BF=CF,利用角平分线的性质易得ET=EG,AT=AG,由勾股定理可得,BT2=BE2-TE2,GC2=EC2-GE2=EC2-TE2,由点F保持在E的右边,且BF=CF,易得BT<GC,可得BT+AT<GC+AG,即AB<AC,由三角形三边关系可得BC的取值范围;法二:如图3,连接FO,过点F作FH∥AE,交AC于H,由平行线的性质和角平分线的性质可得,∠BAE=∠FHO,由中位线的性质可得2FO=AB,∠FOC=2∠FHO,由外角的性质可得∠FOC=∠FHO+∠HFO,易得HO=FO,可得0<FO<4,由三角形三边关系可得AC-AB<BC<AB+AC,设FO=x,则AB=2x,且0<x<4,结合图象,如图4,可得BC的取值范围.
解答 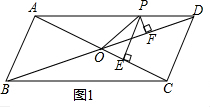 解:(1)如图1,在平行四边形ABCD中,AC=8,BD=12,
解:(1)如图1,在平行四边形ABCD中,AC=8,BD=12,
∴BO=DO=6,AO=CO=4,BC=AD,
又∵AB⊥AC,
∴Rt△ABO中,AB2=62-42=20,
∴AB=2$\sqrt{5}$,
Rt△ABC中,BC2=AB2+AC2=84,
∴BC=2$\sqrt{21}$=AD,
∵点P是线段AD上的动点(不包含端点A,D),
PE⊥AC于点E,PF⊥BD于点F,PE=x,
PF=y,连接OP,
S△POA=$\frac{1}{2}×OA×PE$=2x,
S△POD=$\frac{1}{2}×OD×PF$=3y,
S△AOD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×\frac{1}{2}×2\sqrt{5}×8$=4$\sqrt{5}$,
S△AOD=S△POA+S△POD=2x+3y=$4\sqrt{5}$,
∴y=$\frac{4\sqrt{5}-2x}{3}$,(0<x<2$\sqrt{5}$);
(2)法一(几何法):如图2,在平行四边形ABCD中,对角线AC和BD交于点O,AC=8,
∵点F为BC中点,则BF=CF,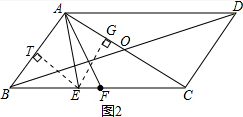
∵AE平分∠BAC,则∠BAE=∠CAE,
过点E作ET⊥AB,EG⊥AC,则ET=EG,AT=AG,
Rt△BTE中,BT2=BE2-TE2,
Rt△EGC中,GC2=EC2-GE2=EC2-TE2,
∵点F保持在E的右边,且BF=CF,
∴BE<EC,
∴BT2<GC2,
∴BT<GC,
∴BT+AT<GC+AG,即AB<AC,即0<AB<8,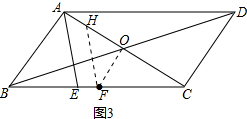
△ABC中,AC-AB<BC<AB+AC,
即0<BC<16;
法二(代数法):在平行四边形ABCD中,对角线AC和BD交于点O,AC=8,
如图3,连接FO,过点F作FH∥AE,交AC于H,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
又∵FH∥AE,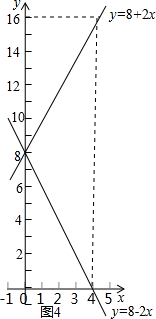
∴∠FHO=∠CAE,
又∵点F为BC中点,BF=CF,AO=CO=4,
∴2FO=AB,FO∥AB,
∴∠FOC=∠BAC,
∴∠FOC=2∠FHO,
又∵∠FOC=∠FHO+∠HFO,
∴∠FHO=∠HFO,
∴HO=FO,
又∵HO<AO,
∴2FO<2AO,且0<FO<4,
∴AB<AC,
∴△ABC中,AC-AB<BC<AB+AC,
设FO=x,则AB=2x,且0<x<4,
∵AC=8,
∴8-2x<BC<8+2x
令y1=8-2x,y2=8+2x,(0<x<4),
画出图象,如图4,可知0<BC<16.
点评 本题主要考查了平行四边形的性质,中位线的性质,三角形三边关系,勾股定理等,利用三角形的面积公式和三角形的三边关系是解答此题的关键.

| A. | (2,7) | B. | (6,3) | C. | (-2,3) | D. | (2,-1) |
| A. | 缩小为原来的$\frac{1}{2}$ | B. | 缩小为原来的$\frac{1}{4}$ | C. | 分式的值不变 | D. | 扩大为原来的2倍 |
| 比赛日期 | 2012-8-4 | 2013-5-21 | 2014-9-28 | 2015-5-20 | 2015-5-31 |
| 比赛地点 | 英国伦敦 | 中国北京 | 韩国仁川 | 中国北京 | 美国尤金 |
| 成绩(秒) | 10.19 | 10.06 | 10.10 | 10.06 | 9.99 |
| A. | 10.06秒,10.06秒 | B. | 10.10秒,10.06秒 | C. | 10.06秒,10.08秒 | D. | 10.08秒,10.06秒 |