题目内容
 如图,点C是直径为4的半圆O上的一个动点(与A、B两点不重合),CD⊥AB于D,点P是线段AC的中点,设BD=x,DP=y.
如图,点C是直径为4的半圆O上的一个动点(与A、B两点不重合),CD⊥AB于D,点P是线段AC的中点,设BD=x,DP=y.(1)求y与x的函数关系式,并写出x的取值范围;
(2)如果∠B=
| 1 |
| 2 |
考点:相似三角形的判定与性质,解一元二次方程-公式法,圆周角定理
专题:
分析:(1)连接OP,由垂径定理得到OP与AC垂直,又CD与AB垂直,得到一对直角相等,再由∠A为公共角,根据两对对应角相等的三角形相似,得到三角形AOP与三角形ACD相似,由相似得比例,再由直角三角形ACD中,P为斜边AC的中点,根据直角三角形斜边上的中线等于斜边的一半得到AP=PD=y,由直径为4得到圆的半径OA=2,且AD=AB-BD=4-x,分别把表示出的各条边代入得到的比例式中,即可得到y与x的关系式,根据x表示线段BD故x大于0,且负数没有平方根得到x小于4(D不与A、B重合,故x不等于4),从而得到函数的定义域;
(2)由∠B=
∠A得到∠A=2∠B,而AP=PD,根据等边对等角得到∠A=∠PDA,故∠PDA=2∠B,又∠PDA为三角形PDB的外角,根据三角形的外角性质得∠PDA=∠B+∠BPD,等量代换得到∠BPD=∠PBD,根据等角对等边得到PD=BD,即y=x,把(1)得到的函数关系式中y换为x,得到关于x的一元二次方程,求出方程的解即可得到BD的长.
(2)由∠B=
| 1 |
| 2 |
解答:解:(1)连接OP,
∵P是AC的中点,
∴OP⊥AC,又CD⊥AB,
∴∠OPA=∠CDA=90°,又∠OAP=∠CAD,
∴△AOP∽△ACD,
∴
=
,
∵P为AC中点,
∴AP=PC=
AC,又CD⊥AD,即△ADC为直角三角形,
∴DP=
AC,又AB=4,DP=y,BD=x,
∴AC=2y,AP=y,AO=2,AD=4-x,
∴
=
,
∴y=
(0<x<4);
(2)当∠B=
∠A时,
∵AP=DP,
∴∠A=∠PDA,
∵∠B=
∠A,即∠A=2∠B,
∴∠PDA=2∠B,又∠PDA为△PDB的外角,
∴∠PDA=∠B+∠BPD,
∴∠B=∠BPD,
∴DP=DB,
即y=x,即x2+x-4=0,
解得:x1=
,x2=
(舍去),
∴BD=
.
∵P是AC的中点,

∴OP⊥AC,又CD⊥AB,
∴∠OPA=∠CDA=90°,又∠OAP=∠CAD,
∴△AOP∽△ACD,
∴
| AP |
| AD |
| AO |
| AC |
∵P为AC中点,
∴AP=PC=
| 1 |
| 2 |
∴DP=
| 1 |
| 2 |
∴AC=2y,AP=y,AO=2,AD=4-x,
∴
| y |
| 4-x |
| 2 |
| 2y |
∴y=
| 4-x |
(2)当∠B=
| 1 |
| 2 |
∵AP=DP,
∴∠A=∠PDA,
∵∠B=
| 1 |
| 2 |
∴∠PDA=2∠B,又∠PDA为△PDB的外角,
∴∠PDA=∠B+∠BPD,
∴∠B=∠BPD,
∴DP=DB,
即y=x,即x2+x-4=0,
解得:x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴BD=
| ||
| 2 |
点评:综合考查了相似三角形的判断与性质,三角形的中位线定理,勾股定理以及一元二次方程的解法,是一道探究型的题,第一问是探究两变量之间的关系,利用垂径定理添加辅助线,构造相似三角形是解本问的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某初三同学绘制出如下两幅不完整的统计图,四个等级奖励的奖品价格用表格表示.
某初三同学绘制出如下两幅不完整的统计图,四个等级奖励的奖品价格用表格表示. 如图,根据下列条件,可以判定哪两条直线平行?并说明判定的根据是什么.
如图,根据下列条件,可以判定哪两条直线平行?并说明判定的根据是什么. 如图,已知A村庄的坐标分别为(2,2),一辆汽车在x轴上行驶,从原点O出发.
如图,已知A村庄的坐标分别为(2,2),一辆汽车在x轴上行驶,从原点O出发.
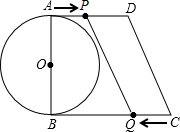 如图所示:在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为⊙O的直径,动点P沿AD方向从点A开始向D以1cm/秒的速度运动,动点Q沿CB方向从点C开始向B以2cm/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.
如图所示:在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为⊙O的直径,动点P沿AD方向从点A开始向D以1cm/秒的速度运动,动点Q沿CB方向从点C开始向B以2cm/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.