题目内容
17.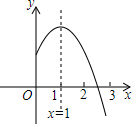 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )| A. | ①、② | B. | ①、③ | C. | ①、②、③ | D. | ①、②、④ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=-1时,y=a-b+c;然后由图象确定当x取何值时,y>0.
解答 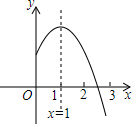 解:①∵开口向下,
解:①∵开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴-$\frac{b}{2a}$>0,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,故正确;
②∵对称轴为直线x=1,抛物线与x轴的一个交点横坐标在2与3之间,
∴另一个交点的横坐标在0与-1之间;
∴当x=-1时,y=a-b+c<0,故正确;
③∵对称轴x=-$\frac{b}{2a}$=1,
∴2a+b=0,
∴b=-2a,
∵当x=-1时,y=a-b+c<0,
∴a-(-2a)+c=3a+c<0,故正确;
④如图,当-1<x<3时,y不只是大于0.故错误.
∴正确的是①②③.
故选:C.
点评 此题考查图象与二次函数系数之间的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
7.二次函数y=-4x2+2x+1的图象与x轴交点的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无法确定 |
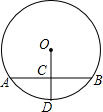 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2.
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2.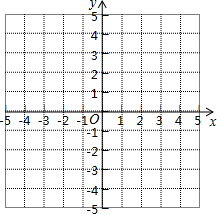 在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
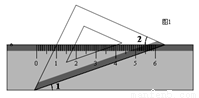
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).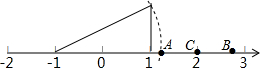 如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$.
如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$. 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°. 已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?