题目内容
7．二次函数y=-4x2+2x+1的图象与x轴交点的个数为（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 无法确定 |
分析 先计算判别式的值，然后根据△=b2-4ac＞0时，抛物线与x轴有2个交点可得到正确选项．
解答 解：∵△=22-4×（-4）×1=20＞0，
∴二次函数y=-4x2+2x+1的图象与x轴有两个交点．
故选C．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程；△=b2-4ac决定抛物线与x轴的交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
相关题目
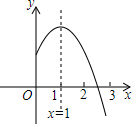二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示，对于下列说法：①abc＜0；②a-b+c＜0； ③3a+c＜0； ④当y＞0时，-1＜x＜3．其中正确的是（ ）
如图，角α的顶点为O，它的一边在x轴的正半轴上，另一边上有一点P（3，4），则sinα=$\frac{4}{5}$．
如图所示，已知∠ABC=30°，∠CBD=80°，BE是∠ABD的平分线，求∠CBE的度数．