题目内容
18.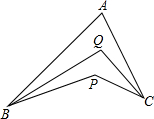 已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)
已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)
分析 连接BC,根据角平分线的性质得到∠3=$\frac{1}{2}∠$ABP,∠4=$\frac{1}{2}∠$ACP,根据三角形的内角和得到∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,求出∠3+∠4=$\frac{1}{2}$(β-α),根据三角形的内角和即可得到结论.
解答  解:连接BC,
解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=$\frac{1}{2}∠$ABP,∠4=$\frac{1}{2}∠$ACP,
∵∠1+∠2=180°-β,2(∠3+∠4)+(∠1+∠2)=180°-α,
∴∠3+∠4=$\frac{1}{2}$(β-α),
∵∠BQC=180°-(∠1+∠2)-(∠3+∠4)=180°-(180°-β)-$\frac{1}{2}$(β-α),
即:∠BQC=$\frac{1}{2}$(α+β).
故答案为:$\frac{1}{2}$(α+β).
点评 本题考查了三角形的内角和,角平分线的定义,连接BC构造三角形是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
7.代数式$\frac{{\sqrt{x}}}{x-1}$有意义的条件是( )
| A. | x≠1 | B. | x≥0 | C. | x≥0且x≠1 | D. | 任意实数 |
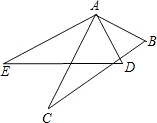 如图,已知△ABC≌△ADE,B和D,C和E是对应顶点,那么BC的对应边是DE.
如图,已知△ABC≌△ADE,B和D,C和E是对应顶点,那么BC的对应边是DE.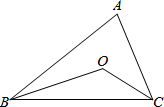 如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:
如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答: