题目内容
16.把下列各分式通分:(1)$\frac{2a}{-3ab}$,$\frac{b}{15{a}^{2}bc}$
(2)$\frac{2xy}{(x+y)^{2}}$,$\frac{x}{{x}^{2}-{y}^{2}}$
(3)$\frac{1}{2{a}^{2}b}$,$\frac{3}{4a{b}^{2}}$,$\frac{5}{6a{c}^{2}}$
(4)$\frac{1}{x-1}$,$\frac{1}{x+1}$,$\frac{3x}{{x}^{2}-1}$.
分析 将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂,找出公因式,再进行变形即可.
解答 解:(1)$\frac{2a}{-3ab}$=-$\frac{10{a}^{2}c}{15{a}^{2}bc}$,$\frac{b}{15{a}^{2}bc}$;
(2)$\frac{2xy}{(x+y)^{2}}$=$\frac{2xy(x-y)}{(x+y)^{2}(x-y)}$,$\frac{x}{{x}^{2}-{y}^{2}}$=$\frac{x(x+y)}{(x+y)^{2}(x-y)}$;
(3)$\frac{1}{2{a}^{2}b}$=$\frac{6b{c}^{2}}{12{a}^{2}{b}^{2}{c}^{2}}$,$\frac{3}{4a{b}^{2}}$=$\frac{9a{c}^{2}}{12{a}^{2}{b}^{2}{c}^{2}}$,$\frac{5}{6a{c}^{2}}$=$\frac{10a{b}^{2}}{12{{a}^{2}b}^{2}{c}^{2}}$;
(4)$\frac{1}{x-1}$=$\frac{x+1}{(x+1)(x-1)}$,$\frac{1}{x+1}$=$\frac{x-1}{(x+1)(x-1)}$,$\frac{3x}{{x}^{2}-1}$=$\frac{3x}{(x+1)(x-1)}$.
点评 此题考查了通分,解答此题的关键是熟知找公分母的方法:
(1)系数取各系数的最小公倍数;
(2)凡出现的因式都要取;
(3)相同因式的次数取最高次幂.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
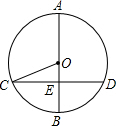 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.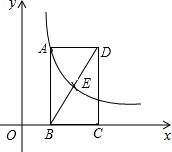 如图,矩形ABCD的边BC在x轴上,E是对角线BD的中点,点E的横坐标为m,A、E是函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,且该函数图象经过点(1,3).
如图,矩形ABCD的边BC在x轴上,E是对角线BD的中点,点E的横坐标为m,A、E是函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,且该函数图象经过点(1,3).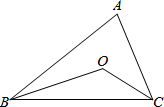 如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:
如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答: