题目内容
17.计算:(1)$\frac{2{x}^{3}}{y}$÷$\frac{4x}{3{y}^{2}}$=$\frac{3{x}^{2}y}{2}$;
(2)$\frac{{x}^{2}-1}{y}$÷$\frac{x+1}{y}$=x-1;
(3)(ab-b2)÷$\frac{{a}^{2}-{b}^{2}}{a+b}$=b.
分析 原式各项利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{2{x}^{3}}{y}$•$\frac{3{y}^{2}}{4x}$=$\frac{3{x}^{2}y}{2}$;
(2)原式=$\frac{(x+1)(x-1)}{y}$•$\frac{y}{x+1}$=x-1;
(3)原式=b(a-b)•$\frac{a+b}{(a+b)(a-b)}$=b,
故答案为:(1)$\frac{3{x}^{2}y}{2}$;(2)x-1;(3)b
点评 此题考查了分式的乘除法,分式乘除法的关键是约分,约分的关键是找出公因式.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
7.-3是3的( )
| A. | 倒数 | B. | 绝对值 | C. | 相反数 | D. | 平方 |
7.若二次函数的解析式为y=2x2-4x+3,则其函数图象与x轴交点的情况是( )
| A. | 没有交点 | B. | 有一个交点 | C. | 有两个交点 | D. | 以上都不对 |
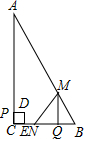 如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).
如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).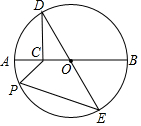 如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.