题目内容
6.计算:(1)20150-$\root{3}{-64}$-|1-$\sqrt{3}$|
(2)6$\sqrt{14}$÷8$\sqrt{18}$
(3)3÷$\sqrt{3}$×$\frac{1}{\sqrt{3}}$
(4)2$\sqrt{x{y}^{3}}$÷(-$\frac{1}{2}$$\sqrt{{x}^{3}{y}^{2}}$)(x≥0,y≥0)
分析 (1)根据0指数幂及数的开方法则、绝对值的性质分别计算出各数,再根据实数的加减法则进行计算即可;
(2)、(4)把根号外的数与被开方数分别相除,再把结果相乘即可;
(3)从左到右依次计算即可.
解答 解:(1)原式=1-(-4)-($\sqrt{3}$-1)
=1+4-$\sqrt{3}$+1
=6-$\sqrt{3}$;
(2)原式=(6÷8)×($\sqrt{14}$÷$\sqrt{18}$)
=$\frac{3}{4}$×$\sqrt{\frac{7}{9}}$
=$\frac{3}{4}$×$\frac{\sqrt{7}}{3}$
=$\frac{\sqrt{7}}{4}$;
(3)原式=3×$\frac{1}{\sqrt{3}}$×$\frac{1}{\sqrt{3}}$
=1;
(4)原式=2×(-2)×$\sqrt{\frac{x{y}^{3}}{{x}^{3}{y}^{2}}}$
=-4$\sqrt{\frac{y}{{x}^{2}}}$
=-$\frac{4\sqrt{y}}{x}$.
点评 本题考查的是实数的运算,熟知0指数幂及数的开方法则、绝对值的性质、二次根式的乘除法则是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.$\sqrt{{4}^{2}}$的平方根是( )
| A. | 4 | B. | 2 | C. | ±4 | D. | ±2 |
18.下列计算结果中,正确的是( )
| A. | (-9)÷(-3)2=1 | B. | (-9)2÷(-32)=-9 | C. | -(-2)3×(-3)2=1 | D. | -(-2)6×(-3)2=-8 |
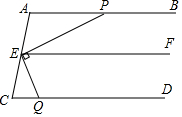 完成下面推理过程.在括号内的横线上填空或填上推理依据.
完成下面推理过程.在括号内的横线上填空或填上推理依据. 如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E.