题目内容
如图,在长方形OABC中,点A、C的坐标分别为(6,0)、(0,4),点D是线段BC上的动点(与端点B不重和),过点D作直线y=-2x+b交折线OAB于点E.
(1)当点D为线段BC的中点时,求b的值;
(2)当点E在线段OA上时,记△ODE的面积为S,求S与b的函数关系式;
(3)探究△ODE的面积是否存在最大值,若存在,求出此时D的坐标;若不存在,请说明理由.

(1)当点D为线段BC的中点时,求b的值;
(2)当点E在线段OA上时,记△ODE的面积为S,求S与b的函数关系式;
(3)探究△ODE的面积是否存在最大值,若存在,求出此时D的坐标;若不存在,请说明理由.

考点:一次函数综合题
专题:
分析:(1)当D为BC中点时,可求得D点坐标,代入直线y=-2x+b可求得b的值;
(2)在直线y=-2x+b中令y=0可用b表示出OE的长度,进一步可表示出△DOE的面积,可得到S和b的关系式;
(3)由条件可知当OE最大时,△ODE的面积最大,此时可求得其最大值,代入直线y=-2x+b可求得b,则可求得D的坐标.
(2)在直线y=-2x+b中令y=0可用b表示出OE的长度,进一步可表示出△DOE的面积,可得到S和b的关系式;
(3)由条件可知当OE最大时,△ODE的面积最大,此时可求得其最大值,代入直线y=-2x+b可求得b,则可求得D的坐标.
解答:解:(1)∵A、C的坐标分别为(6,0)、(0,4),
∴B的坐标为(6,4),
∴当D为BC中点时,其坐标为(3,4),
又∵D点在直线y=-2x+b上,代入可得4=-6+b,
解得b=10,
即当D为BC中点时,b的值为10;
(2)在y=-2x+b中令y=0可得:0=-2x+b,解得x=
,
∴E点坐标(
,0),
∴OE=
,
又∵OA∥BC,
∴D到OE的距离为OC,即△ODE底边OE上的高为4,
∴S=
•
×4=b;
即S与b的关系式为:S=b;
(3)∵D到OE的距离为4,
∴当OE最大值,△ODE的面积最大,此时OE=OA=6,
∴Smax=
×6×4=12,
由(2)可知此时b=12,
∴直线解析式为y=-2x+12,
又∵D点的纵坐标y=4,代入可得4=-2x+12,解得x=4,
∴此时D点的坐标为(4,4).
∴B的坐标为(6,4),
∴当D为BC中点时,其坐标为(3,4),
又∵D点在直线y=-2x+b上,代入可得4=-6+b,
解得b=10,
即当D为BC中点时,b的值为10;
(2)在y=-2x+b中令y=0可得:0=-2x+b,解得x=
| b |
| 2 |
∴E点坐标(
| b |
| 2 |
∴OE=
| b |
| 2 |
又∵OA∥BC,
∴D到OE的距离为OC,即△ODE底边OE上的高为4,
∴S=
| 1 |
| 2 |
| b |
| 2 |
即S与b的关系式为:S=b;
(3)∵D到OE的距离为4,
∴当OE最大值,△ODE的面积最大,此时OE=OA=6,
∴Smax=
| 1 |
| 2 |
由(2)可知此时b=12,
∴直线解析式为y=-2x+12,
又∵D点的纵坐标y=4,代入可得4=-2x+12,解得x=4,
∴此时D点的坐标为(4,4).
点评:本题主要考查待定系数法求函数解析式和矩形的性质、三角形的面积等知识的综合应用,在(1)中确定出D点的坐标是解题的关键,在(2)中利用b表示出OE的长度是解题的关键,在(3)中确定出当△ODE面积有最大值时E点的位置是解题的关键.本题难度不大,属于基础性知识的综合,注重了基础知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果60m表示“向东走60m”,那么“向西走40m”可以表示为( )
| A、-20m | B、-40m |
| C、20m | D、40m |
 如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于
如图,在⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,DE=3,∠BAC+∠EAD=180°,BC=5,则⊙A的半径等于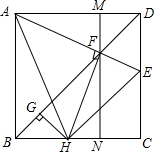 已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
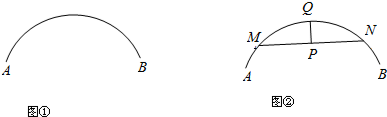
 如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)
如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹) a、b在数轴上的位置如图所示,那么化简|b-a|的结果是
a、b在数轴上的位置如图所示,那么化简|b-a|的结果是 矩形ABCO的顶点A,C分别在x,y轴的正半轴,点D为对角线OB的中点,点E(4,n)在AB上,反比例函数y=
矩形ABCO的顶点A,C分别在x,y轴的正半轴,点D为对角线OB的中点,点E(4,n)在AB上,反比例函数y=