题目内容
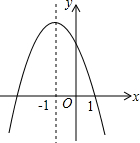 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )| A、3个 | B、4个 | C、5个 | D、6个 |
考点:二次函数图象与系数的关系
专题:
分析:①根据抛物线开口向下判断出a<0;
②根据抛物线的对称轴在y轴左侧确定出ab>0,根据抛物线与y轴的正半轴相交确定出c>0,再根据有理数的乘法运算的符号运算法则解答;
③根据x=1时的函数值是0判断;
④根据x=-1时的函数值是正数判断;
⑤根据抛物线的对称轴为x=-1,得出x=-2与x=0时的函数值相等,由x=0时,y>0,得出x=-2时,y>0,由此判断即可;
⑥由二次函数y=ax2+bx+c的对称轴为x=-1,与x轴交于点(1,0),得出与x轴另一交点是(-3,0),再根据抛物线开口向下,即可得出ax2+bx+c<0的解集是x>1或x<-3.
②根据抛物线的对称轴在y轴左侧确定出ab>0,根据抛物线与y轴的正半轴相交确定出c>0,再根据有理数的乘法运算的符号运算法则解答;
③根据x=1时的函数值是0判断;
④根据x=-1时的函数值是正数判断;
⑤根据抛物线的对称轴为x=-1,得出x=-2与x=0时的函数值相等,由x=0时,y>0,得出x=-2时,y>0,由此判断即可;
⑥由二次函数y=ax2+bx+c的对称轴为x=-1,与x轴交于点(1,0),得出与x轴另一交点是(-3,0),再根据抛物线开口向下,即可得出ax2+bx+c<0的解集是x>1或x<-3.
解答:解:①∵二次函数y=ax2+bx+c的图象开口向下,
∴a<0,故本小题正确;
②∵二次函数y=ax2+bx+c的对称轴x=-
<0,
∴ab>0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∴abc>0,故本小题正确;
③由图形可知,当x=1时,y=0,
即a+b+c=0,故本小题正确;
④由图形可知,当x=-1时,y>0,
即a-b+c>0,故本小题正确;
⑤∵抛物线的对称轴为x=-1,
∴x=-2与x=0时的函数值相等,
∵x=0时,y>0,
∴x=-2时,y>0,
即4a-2b+c>0,故本小题错误;
⑥∵二次函数y=ax2+bx+c的对称轴为x=-1,与x轴交于点(1,0),
∴与x轴另一交点是(-3,0),
∴ax2+bx+c<0的解集是x>1或x<-3,故本小题错误;
综上所述,正确的有①②③④共4个.
故选B.
∴a<0,故本小题正确;
②∵二次函数y=ax2+bx+c的对称轴x=-
| b |
| 2a |
∴ab>0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∴abc>0,故本小题正确;
③由图形可知,当x=1时,y=0,
即a+b+c=0,故本小题正确;
④由图形可知,当x=-1时,y>0,
即a-b+c>0,故本小题正确;
⑤∵抛物线的对称轴为x=-1,
∴x=-2与x=0时的函数值相等,
∵x=0时,y>0,
∴x=-2时,y>0,
即4a-2b+c>0,故本小题错误;
⑥∵二次函数y=ax2+bx+c的对称轴为x=-1,与x轴交于点(1,0),
∴与x轴另一交点是(-3,0),
∴ax2+bx+c<0的解集是x>1或x<-3,故本小题错误;
综上所述,正确的有①②③④共4个.
故选B.
点评:本题考查了二次函数图象与系数的关系,熟练掌握二次函数的性质,开口方向、与y轴的交点、对称轴解析式与系数的关系是解题的关键,利用好特殊自变量所对应的函数值也非常重要.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
埃(āi)是光波长度和分子直径的常用计量单位.1埃为一百亿分之一米,其中,一百亿分之一米用科学记数法可表示为( )
| A、1×10-9米 |
| B、1×10-10米 |
| C、0.1×-910米 |
| D、10×10-10米 |
下列各组中两项属于同类项的是( )
| A、-x2y和2xy2 |
| B、2x2y与-x2yz |
| C、3m3n和-nm3 |
| D、2n2m与-2m2n |
已知点A(3,b)在第一象限,那么点B(3,-b)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
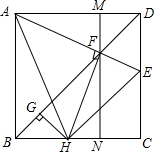 已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD.
已知:如图正方形ABCD中,AE与BD交于F,过点F作MN∥AB,交AD于M,交BC于点N,FH⊥AE,HG⊥BD. 如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)
如图,已知线段a,求作直角三角形,使一直角边长为a,斜边为2a(只留作图痕迹)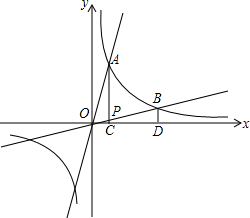 已知反比例函数y=
已知反比例函数y=