题目内容
16．
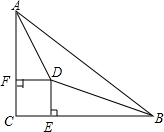如图，在Rt△ABC中，∠C=90°，∠CAB，∠ABC的平分线交于点D，DE⊥BC于E，DF⊥AC于F，请判断四边形CEDF的形状并说明理由．
分析 过D作DG⊥AB于G，由角平分线的性质可求出DF=DE，由正方形的判定定理即可解答．．
解答 解：四边形CEDF是正方形．
过D作DG⊥AB于G，
∵AD、BD是∠CAB、∠CBA的平分线，
∴DF=DG，DE=DG，
∴DF=DE，
∵△ABC是直角三角形，∠C=90°，DE⊥BC于E，DF⊥AC于F，
∴四边形CEDF是正方形．
点评 本题考查了角平分线的性质．三角形内角和定理．正方形的判定定理，涉及面较广，但难度适中．
练习册系列答案
相关题目
2．据报道，到2020年北京地铁规划线网将由19条线路组成，总长度将达到561500米，将561500用科学记数法表示为（ ）
| A． | 0.5615×106 | B． | 5.615×105 | C． | 56.15×104 | D． | 561.5×103 |
7．
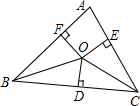如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF=OD=OE，若∠BAC=100°，则∠BOC等于（ ）
如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF=OD=OE，若∠BAC=100°，则∠BOC等于（ ）| A． | 140° | B． | 145° | C． | 150° | D． | 155° |
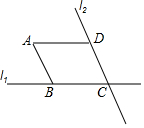如图，直线l1与直线l2相交于点C，点B，D分别在l1，l2上，且BC=CD=3，分别过点B，D作l2，l1的平行线相交于点A．若点A到直线l1的距离为2，则点A到直线l2的距离为2．
已知，如图，在△ABC中，∠A=55°，∠B=95°，将纸片的一角折叠，使点C落在△ABC外．若∠2=25°，则∠1的度数为85°．