题目内容
17. 已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.
分析 (1)由于二次函数过点A,从而可知c=2-2b,然后将c代入抛物线的解析式中即可求出抛物线的顶点坐标.
(2)根据解析式可求出MN=$\frac{1}{2}$(b-2)2,由于点B的位置不确定,需要分情况讨论,求出b的值,从而求出二次函数的解析式,然后求出B、C的坐标后即可求出tan∠ACB.
解答 解:(1)∵二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过点A(2,0),
∴0=-$\frac{1}{2}$×4+2b+c
∴c=2-2b
∴y=-$\frac{1}{2}$x2+bx+c=-$\frac{1}{2}$x2+bx+2-2b
=-$\frac{1}{2}$(x-b)2+$\frac{{b}^{2}-4b+4}{2}$
∴顶点M的坐标为(b,$\frac{{b}^{2}-4b+4}{2}$)
(2)∵tan∠MAN=$\frac{MN}{AN}$=2
∴MN=2AN.
∵M(b,$\frac{{b}^{2}-4b+4}{2}$)
∴N(b,0),
∴MN=$\frac{1}{2}$(b-2)2
①当点B在点N左侧时,AN=2-b,
∴$\frac{1}{2}$(b-2)2=2(2-b)
∴b=-2.不符合题意.
②当点B在点N右侧时,AN=b-2,
∴$\frac{1}{2}$(b-2)2=2(b-2)
∴b=6
∴二次函数的解析式为y=-$\frac{1}{2}$x2+6x-10
∴点C(0,-10),
∵点A、B关于直线MN对称,
∴点B(10,0).
∵OB=OC=10,
∴BC=10,∠OBC=45°,
过点A作AH⊥BC,垂足为H,
∵AB=8,∴AH=BH=4$\sqrt{2}$,∴CH=6$\sqrt{2}$
∴tan∠ACB=$\frac{AH}{CH}$=$\frac{4\sqrt{2}}{6\sqrt{2}}$=$\frac{2}{3}$
点评 本题考查二次函数的综合问题,解题的关键是根据题意求出二次函数的解析式,然后根据锐角三角函数即可求出tan∠ACB的值,本题属于中等题型.

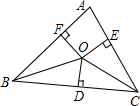 如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=100°,则∠BOC等于( )
如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=100°,则∠BOC等于( )| A. | 140° | B. | 145° | C. | 150° | D. | 155° |
 已知,如图,在△ABC中,∠A=55°,∠B=95°,将纸片的一角折叠,使点C落在△ABC外.若∠2=25°,则∠1的度数为85°.
已知,如图,在△ABC中,∠A=55°,∠B=95°,将纸片的一角折叠,使点C落在△ABC外.若∠2=25°,则∠1的度数为85°.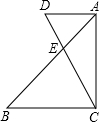 将一副三角板按如图所示的方式摆放,其中∠CAD=∠ACB=90°,∠ACD=30°,∠B=45°,则有下列结论:①AD:BC=AE:CE;②∠BEC=70°;③BC=$\sqrt{3}$AD;④CD:AB=2:$\sqrt{6}$,其中正确结论的序号是③④.(把所有正确结论的序号都填在横线上)
将一副三角板按如图所示的方式摆放,其中∠CAD=∠ACB=90°,∠ACD=30°,∠B=45°,则有下列结论:①AD:BC=AE:CE;②∠BEC=70°;③BC=$\sqrt{3}$AD;④CD:AB=2:$\sqrt{6}$,其中正确结论的序号是③④.(把所有正确结论的序号都填在横线上)