题目内容
2.已知弦AB与CD交于点E,弧$\widehat{BC}$的度数比弧$\widehat{AD}$的度数大20°,若∠CEB=m°,则∠CAB=$\frac{m+10}{2}$(用关于m的代数式表示).分析 由弧BC与AD的度数之差为20°,根据圆周角定理,可得∠CAB-∠C=$\frac{1}{2}$×20°=10°,又由∠CEB=60°,可得∠CAB+∠C=60°,继而求得答案.
解答  解:∵弧BC与AD的度数之差为20°,
解:∵弧BC与AD的度数之差为20°,
∴∠CAB-∠C=$\frac{1}{2}$×20°=10°,
∵∠CEB=∠CAB+∠C=m°,
∴∠CAB=$\frac{m+10}{2}$.
故答案为:$\frac{m+10}{2}$.
点评 此题考查了圆周角定理以及三角形外角的性质.此题难度不大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
13.在下列条件中,△ABC不是直角三角形的是( )
| A. | b2=a2-c2 | B. | a2:b2:c2=1:3:2 | C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
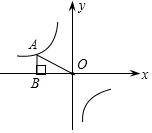 如图,双曲线y=$\frac{k}{x}$(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为3,则该双曲线的表达式为y=-$\frac{6}{x}$.
如图,双曲线y=$\frac{k}{x}$(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为3,则该双曲线的表达式为y=-$\frac{6}{x}$.