Question

11．已知二次函数的图象对称轴为y轴，最大值为0，等边△OAB的顶点A，B均在这个函数的图象上，且AB=4$\sqrt{3}$．
（1）求这个二次函数的表达式；
（2）在这个函数的图象上，是否存在点P，满足S_△OAB=S_△PAB？若存在，试求这点坐标；若不存在，说明理由．

Answer 1

分析 （1）根据对称轴为y轴、最大值为0设解析式为y=ax²，根据等边三角形性质求出点B的坐标，代入解析式求得a的值即可；
（2）由S_△OAB=S_△PAB可得点P的纵坐标，代入解析式求得x的值即可．

解答 解：（1）如图，根据题意，设抛物线解析式为y=ax²，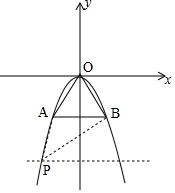

∵△OAB为等边三角形，且AB=OB=4$\sqrt{3}$，
∴点B的横坐标为$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$，纵坐标为-$\frac{\sqrt{3}}{2}$×4$\sqrt{3}$=-6，即B（2$\sqrt{3}$，-6），
将点B（2$\sqrt{3}$，-6）代入y=ax²得：12a=-6，
解得：a=-$\frac{1}{2}$，
∴这个二次函数的表达式为y=-$\frac{1}{2}$x²；

（2）∵S_△OAB=S_△PAB，
∴点P到AB的距离等于6，即点P的纵坐标为-12，
则-$\frac{1}{2}$x²=-12，
解得：x=2$\sqrt{6}$或x=-2$\sqrt{6}$，
即点P的坐标为（2$\sqrt{6}$，-12）或（-2$\sqrt{6}$，-12）．

点评 本题主要考查待定系数法求二次函数解析式及等边三角形的性质，由等边三角形性质求得点B的坐标是解题的关键．