题目内容
7.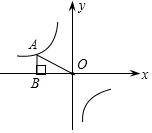 如图,双曲线y=$\frac{k}{x}$(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为3,则该双曲线的表达式为y=-$\frac{6}{x}$.
如图,双曲线y=$\frac{k}{x}$(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为3,则该双曲线的表达式为y=-$\frac{6}{x}$.
分析 先根据反比例函数图象所在的象限判断出k的符号,再根据S△AOB=3求出k的值即可.
解答 解:∵反比例函数的图象在二、四象限,
∴k<0,
∵S△AOB=3,
∴|k|=6,
∴k=-6,即可得双曲线的表达式为:y=-$\frac{6}{x}$,
故答案为:y=-$\frac{6}{x}$.
点评 本题考查的是反比例函数比例系数k的几何意义,即在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{|k|}{2}$,且保持不变.

练习册系列答案
相关题目
17.某股民在上周星期五买进某种股票1000股,每股10元,星期六,星期天股市不交易,下表是本周每日该股票的涨跌情况(单位:元)
(1)本周星期五收盘时,每股是多少元?
(2)已知买进股票时需付买入成交额0.15%的手续费,卖出股票时需付卖出成交额0.25%的交易费,如果在本周五收盘时将全部股票一次性地卖出,那么该股民的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.3 | +0.1 | -0.2 | -0.5 | +0.6 |
(2)已知买进股票时需付买入成交额0.15%的手续费,卖出股票时需付卖出成交额0.25%的交易费,如果在本周五收盘时将全部股票一次性地卖出,那么该股民的收益情况如何?
16.已知a2-5a+1=0,则a+$\frac{1}{a}$-3的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图所示的是某个几何体从三种不同方向所看到的图形.
如图所示的是某个几何体从三种不同方向所看到的图形. 如图,山顶上有高为h的塔BC,从塔顶B测得地面上一点A的俯角是α,从塔底C测得A的俯角为β,求山高H.
如图,山顶上有高为h的塔BC,从塔顶B测得地面上一点A的俯角是α,从塔底C测得A的俯角为β,求山高H.