题目内容
 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求△AEF的面积.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”易证得△ADE≌△ABF;
(2)先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
(2)先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
解答:(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵BC=8,
∴AD=8,
在Rt△ADE中,DE=6,AD=8,
∴AE=
=10,
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90°得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=
AE2=
×100=50.
∴AD=AB,∠D=∠ABC=90°,
而F是CB的延长线上的点,
∴∠ABF=90°,
在△ADE和△ABF中,
|
∴△ADE≌△ABF(SAS);
(2)解:∵BC=8,
∴AD=8,
在Rt△ADE中,DE=6,AD=8,
∴AE=
| AD2+DE2 |
∵△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90°得到,
∴AE=AF,∠EAF=90°,
∴△AEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,旋转的性质以及勾股定理等知识点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
下列等式错误的是( )
| A、(-2)0=1 |
| B、(-1)-2=-1 |
| C、(-2)4÷(-2)2=4 |
| D、(-2)3•(-2)3=26 |

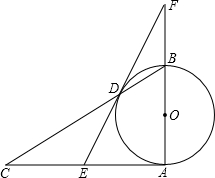 已知:如图,在Rt△ABC中,∠A=90°,以AB为直径作⊙O,BC交⊙O于点D,E是边AC的中点,ED、AB的延长线相交于点F.
已知:如图,在Rt△ABC中,∠A=90°,以AB为直径作⊙O,BC交⊙O于点D,E是边AC的中点,ED、AB的延长线相交于点F. 在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和( 生物学家为了推测最适合某种珍奇植物生长的温度时,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况(如下表).
生物学家为了推测最适合某种珍奇植物生长的温度时,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况(如下表).