题目内容
抛物线y=x2-2x与坐标轴交点为（ ）
| A、二个交点 | B、一个交点 |
| C、无交点 | D、三个交点 |
考点：抛物线与x轴的交点
专题：
分析：当x=0时，求出与y轴的纵坐标；当y=0时，根据一元二次方程x2-2x=0的根的判别式的符号来判定抛物线y=x2-2x与x轴的交点个数．
解答：解：当x=0时，y=0，
则交与原点（0，0）．
当y=0时，x2-2x=0，
△=4＞0，
则该抛物线与x轴有2个交点．
故选：A．
则交与原点（0，0）．
当y=0时，x2-2x=0，
△=4＞0，
则该抛物线与x轴有2个交点．
故选：A．
点评：本题考查了抛物线与x轴交点．注意，本题求得是“抛物线y=x2-2x与两坐标轴的交点个数”，而非“抛物线y=x2-2x与x轴交点的个数”．
练习册系列答案
黄冈创优卷系列答案
相关题目
如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB=DE，此时恰有∠ADE=
如图，已知⊙O1的半径为1cm，⊙O2的半径为4cm，将⊙O1，⊙O2放置在直线l上，如果⊙O1在直线l上任意滚动，那么圆心距O1O2的长不可能是（ ）| A、6cm | B、5cm |
| C、3cm | D、2cm |
下列等式错误的是（ ）
| A、（-2）0=1 |
| B、（-1）-2=-1 |
| C、（-2）4÷（-2）2=4 |
| D、（-2）3•（-2）3=26 |
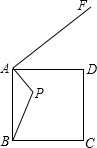已知点P是边长为5的正方形ABCD内一点，且AP=2，AF⊥AP，垂足是点A，若在射线AF上找一点M，使以点A，M，D为顶点的三角形与△ABP相似，则AM为（ ）| A、2 | ||
| B、5 | ||
C、2或
| ||
D、2或
|
一个圆锥的三视图如图，则此圆锥的侧面积为（ ）
| A、15πcm2 |
| B、30πcm2 |
| C、45πcm2 |
| D、55πcm2 |
下列说法正确的是（ ）
A、
| ||||||||
B、（
| ||||||||
C、
| ||||||||
D、
|
在平面直角坐标系xOy中，二次函数y=2x2+bx+c的图象经过（-1，0）和（