题目内容
 已知关于m的方程
已知关于m的方程| 1 |
| 2 |
(1)求m、n的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使
| AP |
| PB |
考点:同解方程,两点间的距离
专题:
分析:(1)先求出方程
(m-16)=-5的解,然后把m的值代入方程2(x-3)-n=3,求出n的值;
(2)分两种情况:①点P在线段AB上,先由AB=6,
=3,求出AP=
,BP=
,然后由点Q为PB的中点,可求PQ=BQ=
BP=
,最后由AQ=AP+PQ即可求出答案;
②点P在线段AB的延长线上,先由AB=6,
=3,求出PB=3,然后点Q为PB的中点,可求PQ=BQ=
,最后由AQ=AB+BQ即可求出答案.
| 1 |
| 2 |
(2)分两种情况:①点P在线段AB上,先由AB=6,
| AP |
| PB |
| 9 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
②点P在线段AB的延长线上,先由AB=6,
| AP |
| PB |
| 3 |
| 2 |
解答:解:(1)
(m-16)=-5,
m-16=-10,
m=6,
∵关于m的方程
(m-16)=-5的解也是关于x的方程2(x-3)-n=3的解.
∴x=m,
将m=6,代入方程2(x-3)-n=3得:
2(6-3)-n=3,
解得:n=3,
故m=6,n=3;
(2)由(1)知:AB=6,
=3,
①当点P在线段AB上时,如图所示:

∵AB=6,
=3,
∴AP=
,BP=
,
∵点Q为PB的中点,
∴PQ=BQ=
BP=
,
∴AQ=AP+PQ=
+
=
;
②当点P在线段AB的延长线上时,如图所示:

∵AB=6,
=3,
∴PB=3,
∵点Q为PB的中点,
∴PQ=BQ=
,
∴AQ=AB+BQ=6+
=
.
故AQ=
或
.
| 1 |
| 2 |
m-16=-10,
m=6,
∵关于m的方程
| 1 |
| 2 |
∴x=m,
将m=6,代入方程2(x-3)-n=3得:
2(6-3)-n=3,
解得:n=3,
故m=6,n=3;
(2)由(1)知:AB=6,
| AP |
| PB |
①当点P在线段AB上时,如图所示:

∵AB=6,
| AP |
| PB |
∴AP=
| 9 |
| 2 |
| 3 |
| 2 |
∵点Q为PB的中点,
∴PQ=BQ=
| 1 |
| 2 |
| 3 |
| 4 |
∴AQ=AP+PQ=
| 9 |
| 2 |
| 3 |
| 4 |
| 21 |
| 4 |
②当点P在线段AB的延长线上时,如图所示:

∵AB=6,
| AP |
| PB |
∴PB=3,
∵点Q为PB的中点,
∴PQ=BQ=
| 3 |
| 2 |
∴AQ=AB+BQ=6+
| 3 |
| 2 |
| 15 |
| 2 |
故AQ=
| 21 |
| 4 |
| 15 |
| 2 |
点评:此题考查了一元一次方程的解,以及两点间的距离,熟练掌握运算法则是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列四种说法中正确的是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
| A、①② | B、①④ |
| C、①②④ | D、①②③④ |
 从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )
从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )| A、圆锥 | B、圆柱 |
| C、三棱锥 | D、三棱柱 |
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:①∠DEC=60°;②△ACD≌△ACE;③△CDE为等边三角形;
其中正确的结论是( )
| A、①② | B、①③ | C、③ | D、①②③ |
下列长度的三条线段不能组成直角三角形的是( )
| A、3,4,5 | ||||
B、2,
| ||||
C、1,
| ||||
| D、6,10,8 |
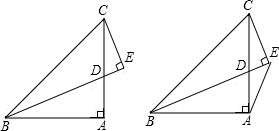 如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.
如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E. 如图,
如图,