题目内容
 如图,点O是△ABC内任意一点,且△ABC为等边三角形,高为3cm,则O到三边的距离之和为?
如图,点O是△ABC内任意一点,且△ABC为等边三角形,高为3cm,则O到三边的距离之和为?考点:等边三角形的性质
专题:
分析:设△ABC的边长为a,过点O分别作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,再连接OA,OB,OC,根据三角形的面积公式求解即可.
解答: 解:设△ABC的边长为a,过点O分别作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,再连接OA,OB,OC,
解:设△ABC的边长为a,过点O分别作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,再连接OA,OB,OC,
∵S△ABC=S△AOB+S△BOC+S△AOC
=
a•OD+
a•OE+
a•OF
=
a(OD+OE+OF)=
a×3,
∴OD+OE+OF=3,即O到三边的距离之和为3.
 解:设△ABC的边长为a,过点O分别作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,再连接OA,OB,OC,
解:设△ABC的边长为a,过点O分别作OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D、E、F,再连接OA,OB,OC,∵S△ABC=S△AOB+S△BOC+S△AOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD+OE+OF=3,即O到三边的距离之和为3.
点评:本题考查的是等边三角形的性质,熟知等边三角形的三条边均相等是解答此题的关键.

练习册系列答案
相关题目
 从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )
从正面、上面、左面三个方向看某一个物体得到的图形如图所示,则这个物体是( )| A、圆锥 | B、圆柱 |
| C、三棱锥 | D、三棱柱 |
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:①∠DEC=60°;②△ACD≌△ACE;③△CDE为等边三角形;
其中正确的结论是( )
| A、①② | B、①③ | C、③ | D、①②③ |
 如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )
如图,当一个点从O出发,沿15°线移动1个单位长度(即OP长为1个单位长度),这个点在竖直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,sin15°约等于( )| A、3.73 | B、0.97 |
| C、0.50 | D、0.26 |
下列等式成立是( )
| A、-2×3=6 | ||
| B、-(-1)=-1 | ||
C、1÷(-3)=
| ||
| D、|-2|=2 |
 写出图中所有同位角、内错角、同旁内角.
写出图中所有同位角、内错角、同旁内角.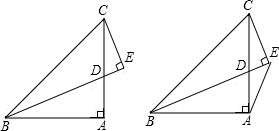 如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.
如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E. 如图,O为直线AB上的一点,OE,OF分别平分∠AOC,∠COB,请问OE⊥OF吗?为什么?
如图,O为直线AB上的一点,OE,OF分别平分∠AOC,∠COB,请问OE⊥OF吗?为什么?