题目内容
3．若n边形的每一个外角都是72°，则边数n为5．分析 先判断出此多边形是正多边形，然后根据正多边形的边数等于360°除以每一个外角的度数计算即可得解．
解答 解：∵多边形的每一个外角都是72°，
∴此多边形是正多边形，
360°÷72°=5，
所以，它的边数是5．
故答案为：5．
点评 本题考查了多边形的内角与外角，熟练掌握正多边形的边数、每一个外角的度数、外角和三者之间的关系是解题的关键．
练习册系列答案
相关题目
13．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{16}$ | B． | $\sqrt{6}$ | C． | $\sqrt{28}$ | D． | $\sqrt{\frac{1}{5}}$ |
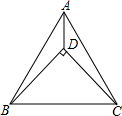如图，等腰直角三角形BDC的顶点D在等边三角形ABC的内部，∠BDC=90°，连接AD，过点D作一条直线将△ABD分割成两个等腰三角形，则分割出的这两个等腰三角形的顶角分别是120，150度．
11．在Rt△ABC中，已知两边长分别是3和4，则第三边长为（ ）
| A． | 5 | B． | $\sqrt{7}$ | C． | 5或$\sqrt{7}$ | D． | 无法确定 |
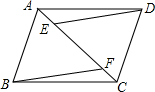如图，已知四边形ABCD中，连接AC，点E、F在AC上，AE=CF，连接DE，BF，且DE$\underset{∥}{=}$BF，求证：四边形ABCD是平行四边形．
______；