题目内容
15.在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性.根据课堂学习的经验,解决下列问题: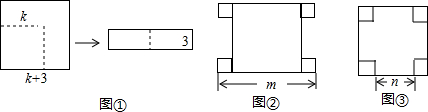
(1)如图①,边长为(k+3)的正方形纸片,剪去一个边长为k的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),则这个长方形的面积是6k+9(用含k的式子表示);
(2)有3张边长为a的正方形纸片,4张边长分别为a,b (a<b) 的长方形纸片,5张边长为b的正方形纸片,现从其中取出若干张纸片(每种纸片至少取一张),拼成一个正方形(不重叠无缝隙),则所拼成的正方形的边长最长可以为D;
A.a+b B.2a+b C.3a+b D.a+2b
(3)一个大正方形和4个大小完全相同的小正方形按图②,图③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积(用含m,n的式子表示).
分析 (1)两个正方形的面积差就是长方形的面积;
(2)根据3张边长为a的正方形纸片的面积是3a2,4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,5张边长为b的正方形纸片的面积是5b2,得出a2+4ab+4b2=(a+2b)2,再根据正方形的面积公式即可得出答案;
(3)利用大正方形的面积减去4个小正方形的面积即可求解.
解答 解:(1)则这个长方形的面积是(k+3)2-k2=6k+9;
(2)3张边长为a的正方形纸片的面积是3a2,
4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,
5张边长为b的正方形纸片的面积是5b2,
∵a2+4ab+4b2=(a+2b)2,
∴拼成的正方形的边长最长可以为(a+2b),
故选:D.
(3)③的大正方形中未被小正方形覆盖部分的面积=($\frac{m+n}{2}$)2-4×($\frac{m-n}{4}$)2=mn.
点评 此题考查整式的混合运算,掌握基本平面图形的面积计算方法是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.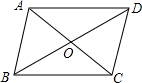 平行四边形ABCD中,AC、BD交于O点,下列条件中,能使四边形ABCD是矩形的是( )
平行四边形ABCD中,AC、BD交于O点,下列条件中,能使四边形ABCD是矩形的是( )
 平行四边形ABCD中,AC、BD交于O点,下列条件中,能使四边形ABCD是矩形的是( )
平行四边形ABCD中,AC、BD交于O点,下列条件中,能使四边形ABCD是矩形的是( )| A. | AC⊥BD | B. | AO=BO | C. | AB=AD | D. | AO=CO |
7.若y=$\sqrt{x-1}$+$\sqrt{1-x}$-2,则-xy的值为( )
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
4. 如图,在边长为$\sqrt{3}$的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为$\sqrt{3}$的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
 如图,在边长为$\sqrt{3}$的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为$\sqrt{3}$的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 1 |

 ,宽为
,宽为 的长方形铁片上,挖去长为
的长方形铁片上,挖去长为 ,宽为
,宽为 的小长方形铁片,求剩余部分面积。
的小长方形铁片,求剩余部分面积。