Question

4．过等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1、3、5．试求这个等边三角形的面积．

Answer 1

分析 作AM⊥BC，根据等边三角形的面积计算可以求得AM=PE+PD+PF，再根据等边三角形的高线长可以计算等边三角形的边长，即可解题．

解答 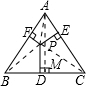解：过A作AM⊥BC，则AM为BC边上的高，
连接PA、PB、PC，
则△ABC的面积S=$\frac{1}{2}$BC•AM=$\frac{1}{2}$（BC•PD+AB•PF+AC•PE），
∴BC•AM=BC•PD+AB•PF+AC•PE，
∵△ABC是等边三角形，
∴AB=BC=AC，
∴BC•AM=BC•PD+BC•PF+BC•PE=BC•（PD+PF+PE），
∴PD+PE+PF=AM，
∴△ABC的高为：AM=1+3+5=9，
∴△ABC的边长为：AB=$\frac{AM}{sin60°}$=$\frac{9}{\frac{\sqrt{3}}{2}}$6$\sqrt{3}$，
∴S_△ABC=$\frac{1}{2}$×6$\sqrt{3}$×9=27$\sqrt{3}$．

点评 本题考查了三角形面积的计算，考查了等边三角形边长和高线长的关系，本题中求AM=PD+PE+PF是解题的关键．